はじめに

　Rによる因果媒介分析のまとめ。今回は媒介変数・アウトカムが連続変数の場合のパラメトリックな手法を扱う。比較的お手軽にできる解析手法だが、同時に厳しい仮定を必要とする手法でもある。なので実際の解析から感度分析による結果の解釈までまとめてみたい。

Baron-Kenny法

　Baron-Kenny法は線形モデルによって媒介効果を推定する手法。アウトカムと媒介変数を応答変数とした2回の回帰分析を行い、媒介効果を推定する。
　今回解析に使用するのはmediationパッケージに入っている、jobsデータ（就職活動に対する介入調査：JOBSⅡ field experetiment）。1801人の非雇用者が事前に質問紙調査を受け、ランダムに介入群と対照群に割り付けられた。介入群は職業技能ワークショップに参加し、対照群は就職活動についてのブックレットが配布された。後にインタビュー調査が行われ、アウトカムとして介入後の抑うつ症状（Hopkins Symptom Checklistスコア）、媒介変数として就職活動自己効力感（連続変数）が測定された。以下では、介入をtreat、媒介変数をjob_seek、アウトカムをdepress2、交絡変数をecon_hard（経済的苦痛）・sex・ageとする。

library(mediation)
data("jobs")

ステップ1：媒介変数に対する回帰分析

　まず媒介変数を応答変数、曝露変数と交絡因子を説明変数とした回帰分析を行う。

model.m <- lm(job_seek ~ treat + econ_hard + sex + age, data=jobs)

ステップ2：アウトカムに対する回帰分析

　次にアウトカムを応答変数、曝露変数、媒介変数、交絡因子を説明変数として回帰分析を実施。

model.y <- lm(depress2 ~ treat + job_seek + econ_hard + sex + age, data=jobs)

ステップ3：媒介効果の点推定値・95%信頼区間の推定

　上記の結果をもとに媒介効果を推定するため、mediate関数を使う。ここでは媒介効果の点推定値と95%信頼区間の推定方法について設定することができる。mediate関数でboot=TRUEとすることでノンパラメトリックブートストラップ法による信頼区間が推定可能（分布を仮定しないが膨大な計算が必要）。

mediate関数 内容
boot=TRUE ノンパラメトリックブートストラップ法による信頼区間
　　 (デフォルト：boot=FALSE)準ベイズ近似による信頼区間
sims=試行回数 シミュレーション回数
treat=“変数” 治療・曝露に該当する変数の指定
mediator=“変数” 媒介変数に該当する変数の指定

準ベイズ近似によるACME推定。

m.out <- mediate(model.m, model.y, sims=100, treat="treat", mediator="job_seek")
summary(m.out)
## 
## Causal Mediation Analysis 
## 
## Quasi-Bayesian Confidence Intervals
## 
##                Estimate 95% CI Lower 95% CI Upper p-value
## ACME            -0.0179      -0.0424         0.00    0.14
## ADE             -0.0468      -0.1212         0.04    0.20
## Total Effect    -0.0646      -0.1496         0.01    0.12
## Prop. Mediated   0.2403      -0.9002         1.63    0.26
## 
## Sample Size Used: 899 
## 
## 
## Simulations: 100
plot(m.out)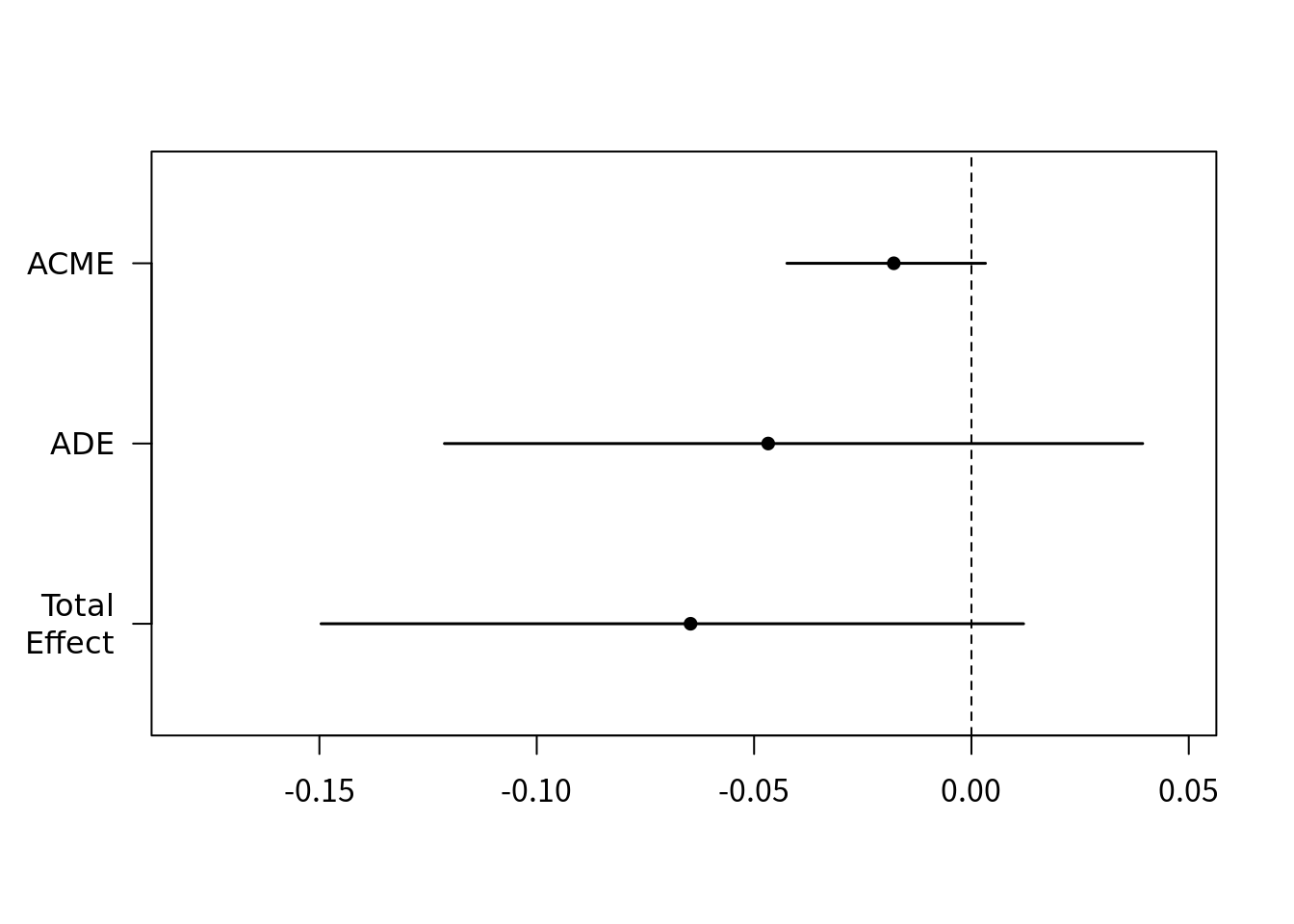

ノンパラメトリックブートストラップ法によるACME推定

m.out <-  mediate(model.m, model.y, boot=TRUE, sims=100, treat="treat", mediator="job_seek")
## Running nonparametric bootstrap
summary(m.out)
## 
## Causal Mediation Analysis 
## 
## Nonparametric Bootstrap Confidence Intervals with the Percentile Method
## 
##                Estimate 95% CI Lower 95% CI Upper p-value
## ACME            -0.0157      -0.0352         0.01    0.18
## ADE             -0.0403      -0.1046         0.03    0.30
## Total Effect    -0.0560      -0.1192         0.02    0.22
## Prop. Mediated   0.2811      -1.4052         1.10    0.28
## 
## Sample Size Used: 899 
## 
## 
## Simulations: 100
plot(m.out)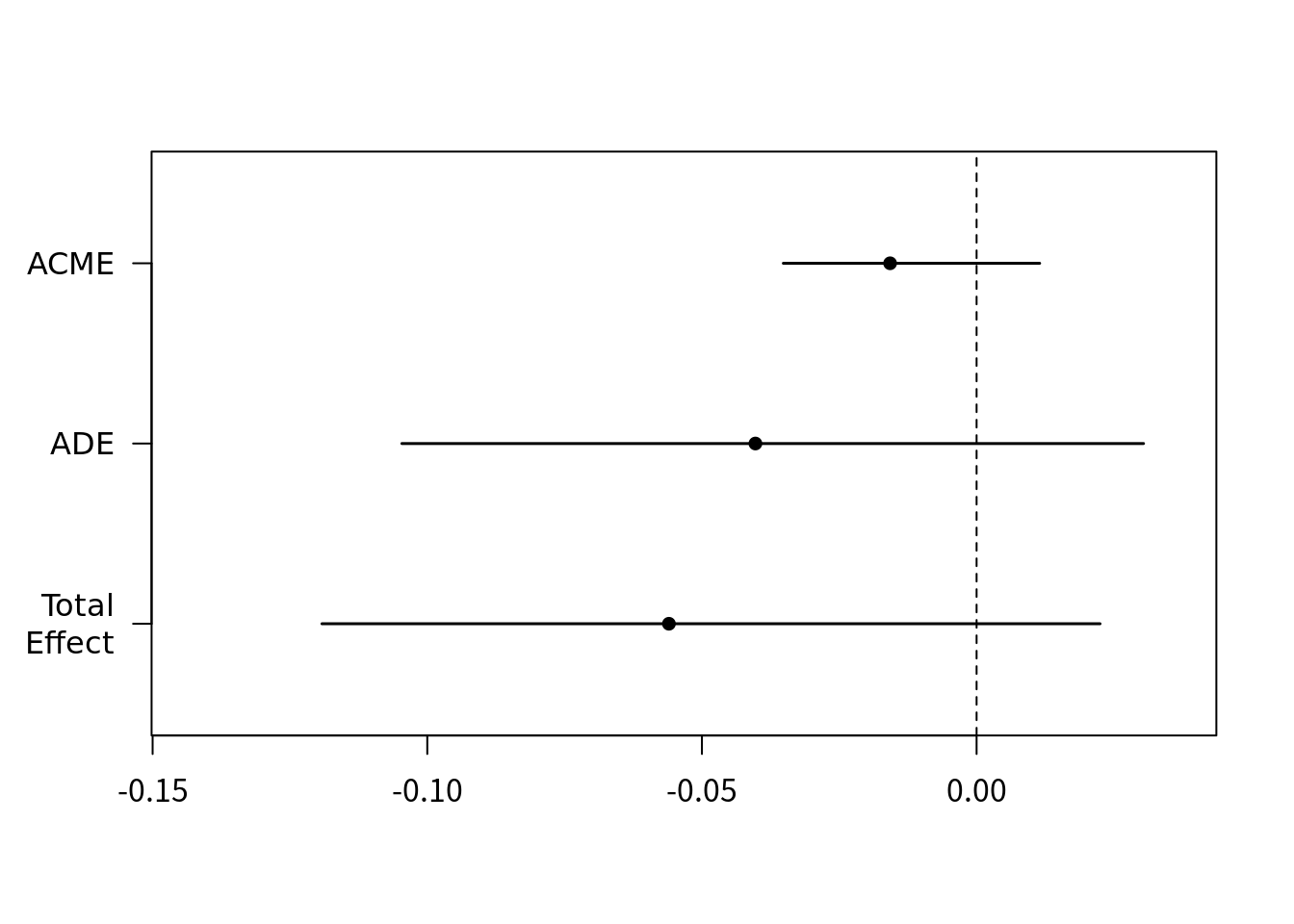

　媒介効果(ACME)を見ると、職業技能ワークショップは就職活動の自己効力感を介して抑うつ症状に影響すると解釈できる（信頼区間が負の大部分を被覆）。

ステップ4：感度分析

　媒介分析では、曝露ーアウトカム間と媒介変数ーアウトカム間の未測定交絡が無いことが仮定される（Imaiらは“Sequential Ignorability”と定義）。しかしこの仮定は非常に厳しいもので、現実には満たされることはないと考えるべき。したがって感度分析によって、どの程度仮定が満たされていないかを定量化する必要がある。ImaiらはBaron-Kenny法・SEMによる媒介分析に対する感度分析を提案している（Imai, K. Statistical Science. 2010; Imai, K. Phycological Science. 2010）。

　感度分析はステップ1回帰分析の残差とステップ2回帰分析の残差の間の相関係数で評価を行う。残差に相関があれば、潜在的な未測定交絡がある可能性があり、推定が妥当でないことが示唆される。また残差の相関係数は解釈が難しいという問題があり、Imaiらは代わりに決定係数による感度分析を提案している（Imai, K. Statistical Science. 2010;）。決定係数により、未測定交絡によってACMEがどの程度影響を受けるかを定量化する。以下では両方の感度分析を行う。
　感度分析は以下のコードで実行できる。sens.par=“R2”で決定係数、指定しなければ相関係数による感度分析の結果がプロットされる。

plot関数 内容
sens.par=“R2” 決定係数による感度分析（デフォルトは相関係数）
r.type=1　　 未測定交絡によって説明される原因不明の分散比率での感度分析
　　　=2 未測定交絡によって説明される元の分散比率での感度分析
sign.prod=1 未測定交絡の係数符号が媒介変数・アウトカムで同じ場合
　　　　=-1 係数の符号が異なるもとでの感度分析 　 
s.out <- medsens(m.out)
summary(s.out)
## 
## Mediation Sensitivity Analysis for Average Causal Mediation Effect
## 
## Sensitivity Region
## 
##        Rho    ACME 95% CI Lower 95% CI Upper R^2_M*R^2_Y* R^2_M~R^2_Y~
##  [1,] -0.9  0.0986      -0.0527       0.2499         0.81       0.7044
##  [2,] -0.8  0.0581      -0.0311       0.1473         0.64       0.5565
##  [3,] -0.7  0.0385      -0.0207       0.0978         0.49       0.4261
##  [4,] -0.6  0.0258      -0.0139       0.0655         0.36       0.3130
##  [5,] -0.5  0.0162      -0.0089       0.0414         0.25       0.2174
##  [6,] -0.4  0.0084      -0.0050       0.0218         0.16       0.1391
##  [7,] -0.3  0.0017      -0.0028       0.0061         0.09       0.0783
##  [8,] -0.2 -0.0044      -0.0122       0.0033         0.04       0.0348
##  [9,] -0.1 -0.0102      -0.0262       0.0059         0.01       0.0087
## [10,]  0.0 -0.0157      -0.0402       0.0087         0.00       0.0000
## [11,]  0.1 -0.0213      -0.0542       0.0116         0.01       0.0087
## [12,]  0.2 -0.0270      -0.0687       0.0146         0.04       0.0348
## [13,]  0.3 -0.0332      -0.0842       0.0178         0.09       0.0783
## [14,]  0.4 -0.0399      -0.1013       0.0214         0.16       0.1391
## [15,]  0.5 -0.0477      -0.1210       0.0256         0.25       0.2174
## [16,]  0.6 -0.0573      -0.1452       0.0307         0.36       0.3130
## [17,]  0.7 -0.0700      -0.1775       0.0375         0.49       0.4261
## [18,]  0.8 -0.0896      -0.2270       0.0479         0.64       0.5565
## [19,]  0.9 -0.1301      -0.3297       0.0695         0.81       0.7044
## 
## Rho at which ACME = 0: -0.3
## R^2_M*R^2_Y* at which ACME = 0: 0.09
## R^2_M~R^2_Y~ at which ACME = 0: 0.0783

　まずsummary()で表示されたテーブルについて。左から順に、残差の相関係数、ACMEの点推定値、ACMEの95%信頼区間下限と上限、未測定交絡によって説明される原因不明の分散比率、未測定交絡によって説明される元の分散比率、を示している。またテーブルの下部では、ACME=0での相関係数、決定係数による指標の値がわかる。これらの詳細な定義式はImaiらの原著論文を参考に。

plot(s.out)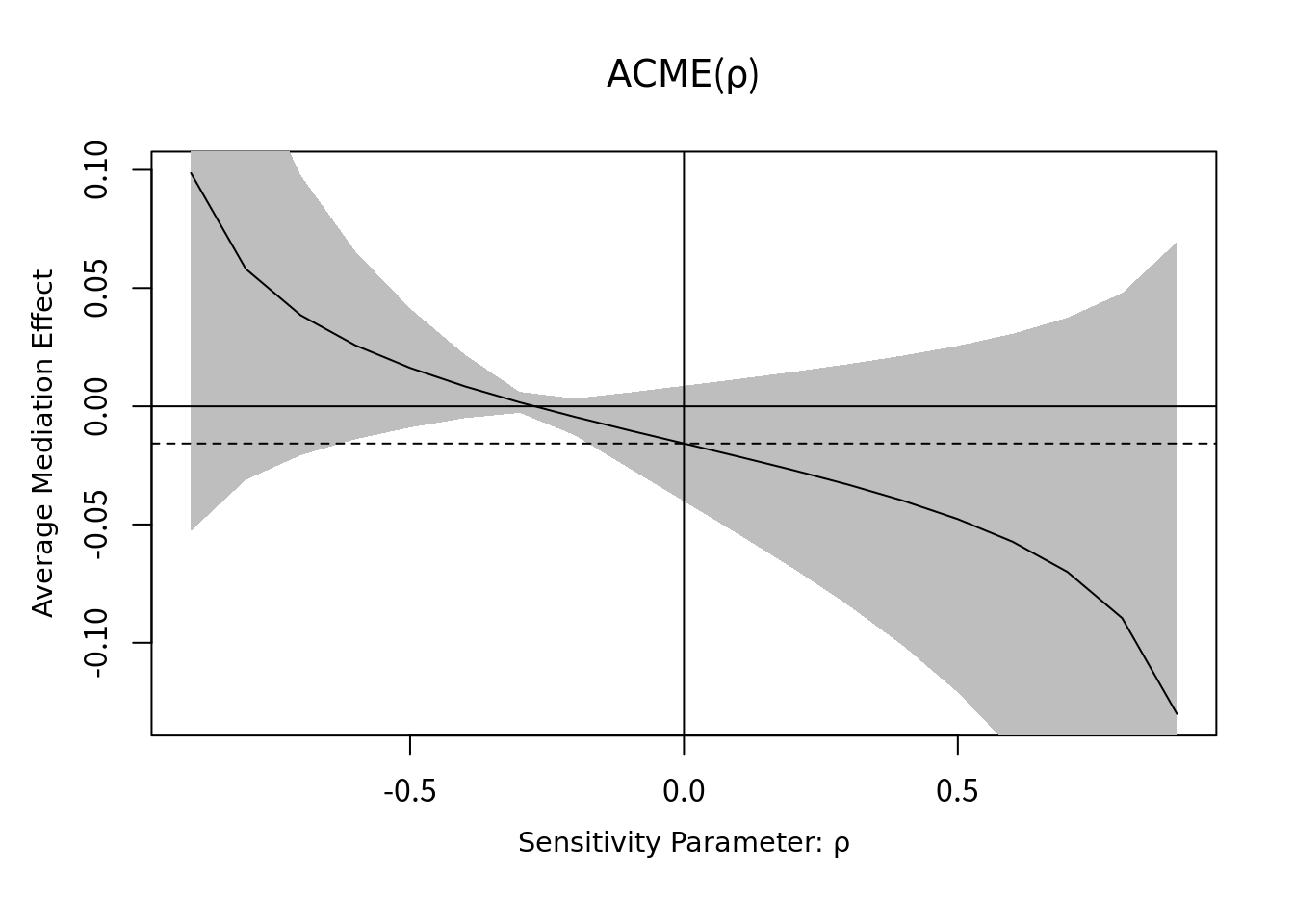

　残差の相関係数による感度分析の結果が上記のグラフ。これにより未測定交絡によってACMEがどの程度影響を受けるのかが視覚的に評価できる。曲線はACMEの点推定値を変化させたときの残差の相関係数、グレーの部分はACMEの95%信頼区間を示す。このグラフより、未測定交絡が媒介変数・アウトカムに対して同じ符号で影響する（正と正、負と負）場合、未測定交絡の影響を考慮しても媒介効果は存在するだろうと考えられる（相関係数<0でACMEの点推定値は常に負の値）。しかし未測定交絡が異なる符号で影響する場合、媒介効果は未測定交絡によって正・負の値両方を取る可能性があり、解析で得られたACMEの値は妥当でないかもしれない。この場合負の媒介効果が存在するという主張の根拠が揺らぐことになる。

plot(s.out, sens.par="R2", r.type=1, sign.prod=-1)

plot(s.out, sens.par="R2", r.type=1, sign.prod=1)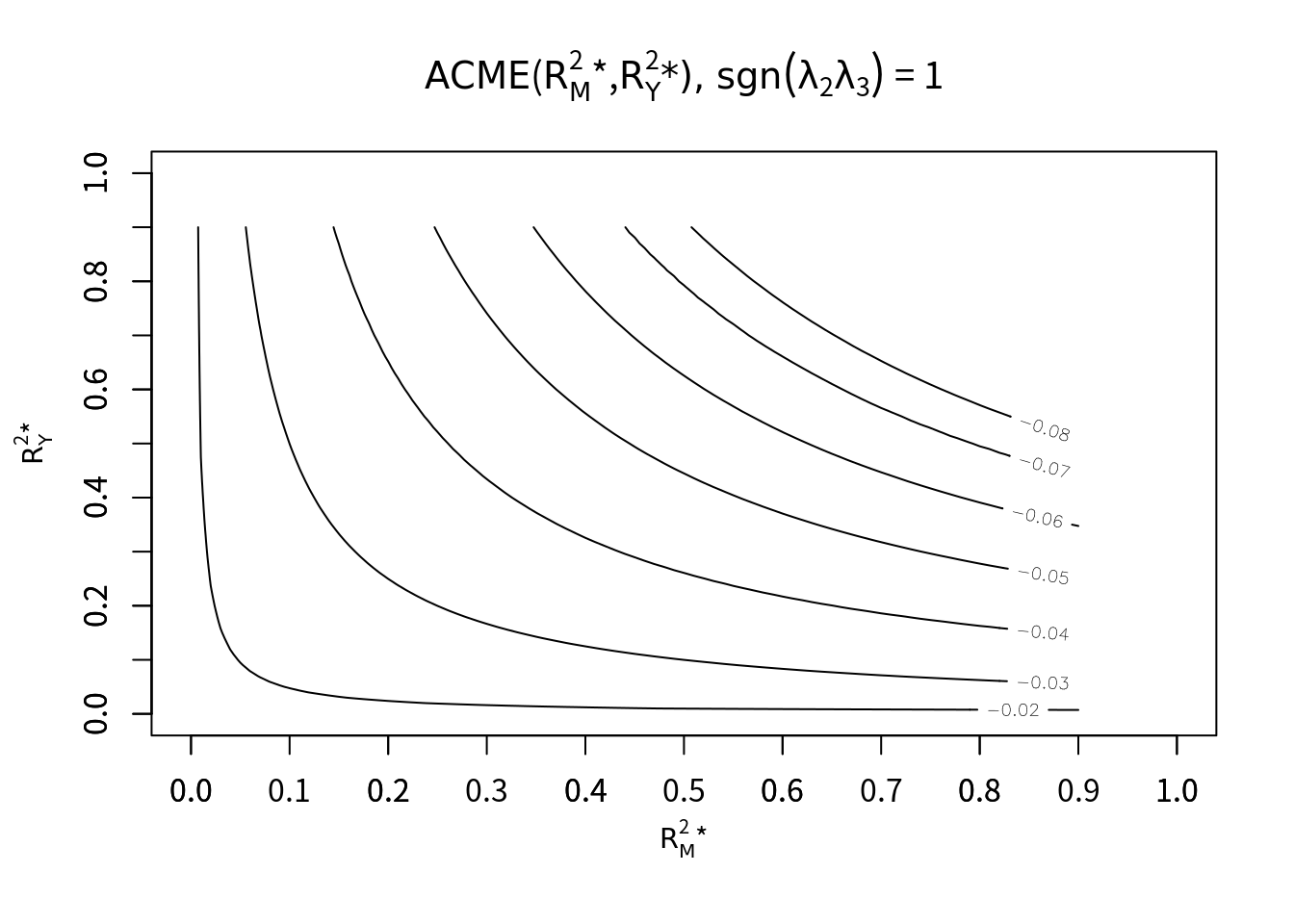

plot(s.out, sens.par="R2", r.type=2, sign.prod=-1)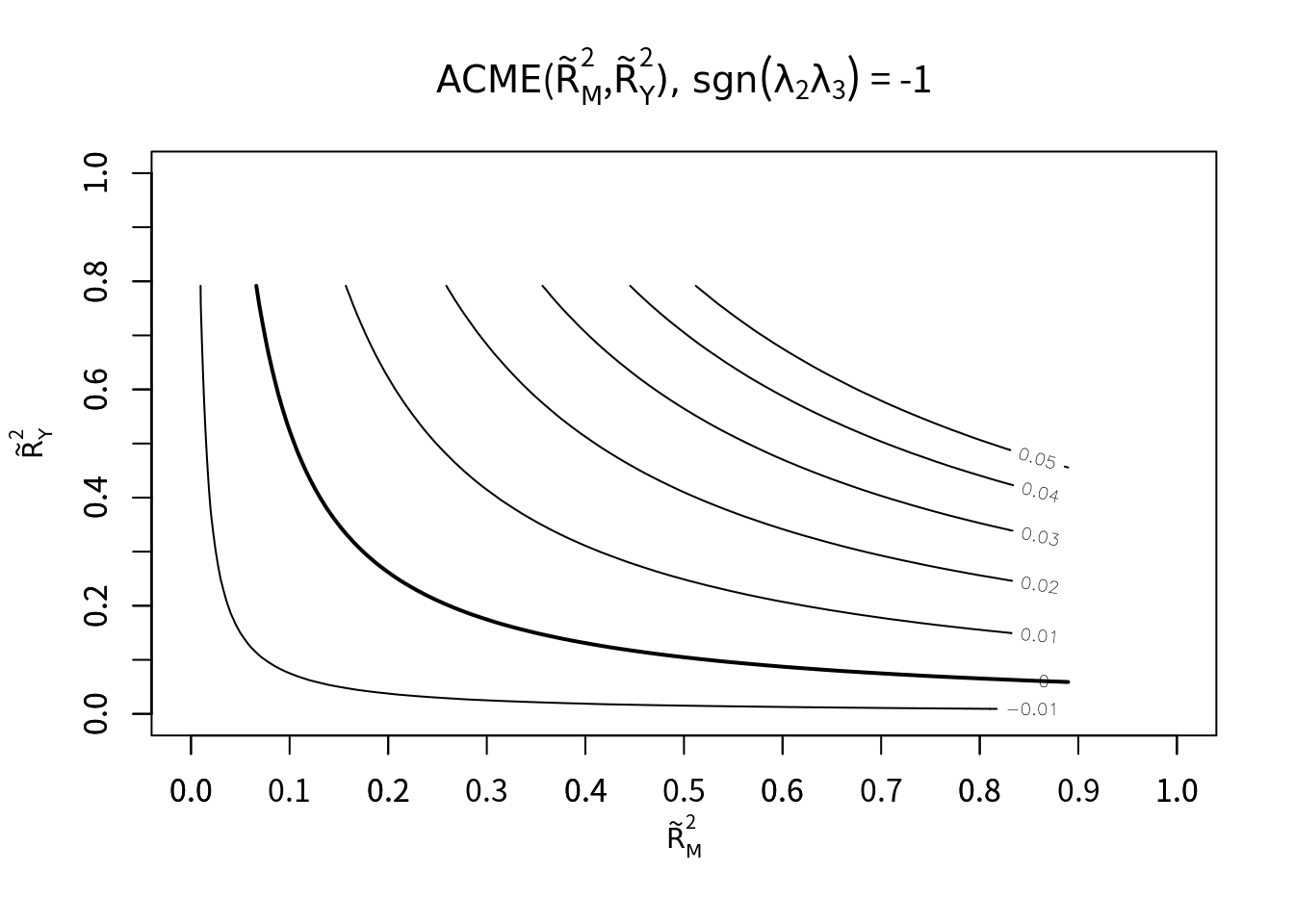

plot(s.out, sens.par="R2", r.type=2, sign.prod=1)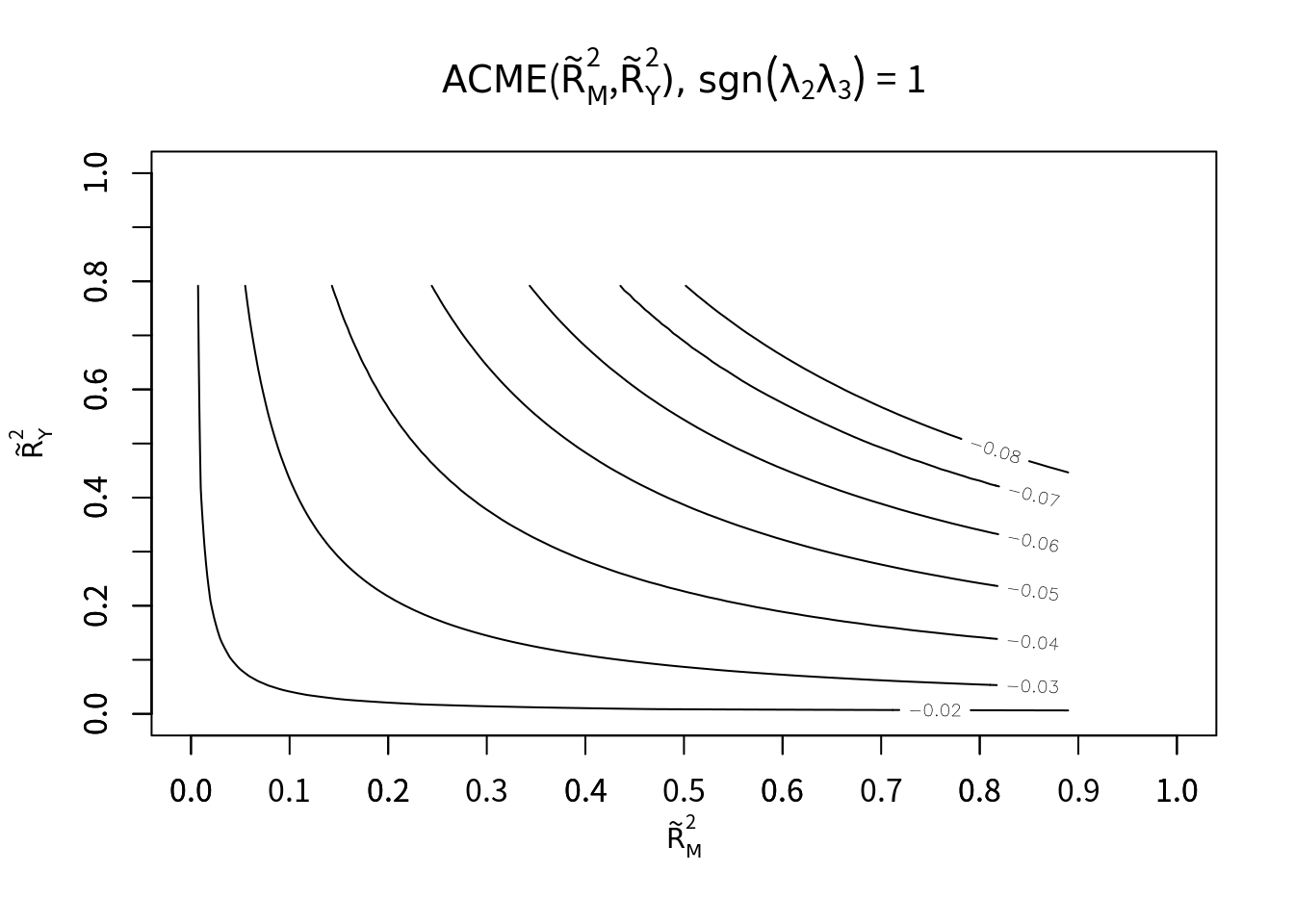

　決定係数による感度分析が上記4つのグラフ。
　1番目のグラフより、未測定交絡の符号が同じという仮定のもとで「未測定交絡によって説明される原因不明の分散比率」が4%以下ならば、解析で得られたACMEは妥当であると判断できる（現実には満たすことは不可能な数値）。また3番目のグラフより、未測定交絡によって説明される元の分散比率が3%以下であれば、解析で得られたACMEは妥当であると判断できる。以上より、未測定交絡が媒介変数・アウトカムに対して異なる符号で相関をもつならば、解析結果は妥当でないと判断すべき。
　その一方で未測定交絡が媒介変数・アウトカムに対して同じ符号で相関をもつならば、解析結果は妥当である（未測定交絡があっても常にACMEは負の値）。
　未測定交絡の符号は研究対象についての専門知識をもとに判断すべきであり、それは統計学の領分ではない。それぞれの分野での専門知識をもとに符号がどちらかを想定することで、解析結果の妥当性を考察できるだろう。

交互作用項の検討

　上記で得られた結果は、交互作用が無いという仮定のもとで得られたものである。しかし現実には、「介入群と対照群で間接効果が同じ」という仮定はあまり現実的なものではない。したがって交互作用については追加で検討しておくのが無難だろう。

治療と媒介変数間の交互作用

model.y1 <- lm(depress2 ~ treat + job_seek + treat:job_seek + econ_hard + sex + age, data=jobs)
m.out1 <- mediate(model.m, model.y1, sims=100, treat="treat", mediator="job_seek")
summary(m.out1)
## 
## Causal Mediation Analysis 
## 
## Quasi-Bayesian Confidence Intervals
## 
##                          Estimate 95% CI Lower 95% CI Upper p-value  
## ACME (control)            -0.0211      -0.0507         0.00    0.08 .
## ACME (treated)            -0.0148      -0.0382         0.00    0.08 .
## ADE (control)             -0.0494      -0.1077         0.02    0.14  
## ADE (treated)             -0.0431      -0.1046         0.02    0.16  
## Total Effect              -0.0642      -0.1320         0.01    0.06 .
## Prop. Mediated (control)   0.3225      -0.2038         1.62    0.14  
## Prop. Mediated (treated)   0.2305      -0.2014         1.73    0.14  
## ACME (average)            -0.0179      -0.0436         0.00    0.08 .
## ADE (average)             -0.0462      -0.1059         0.02    0.16  
## Prop. Mediated (average)   0.2765      -0.2026         1.73    0.14  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Sample Size Used: 899 
## 
## 
## Simulations: 100
plot(m.out1)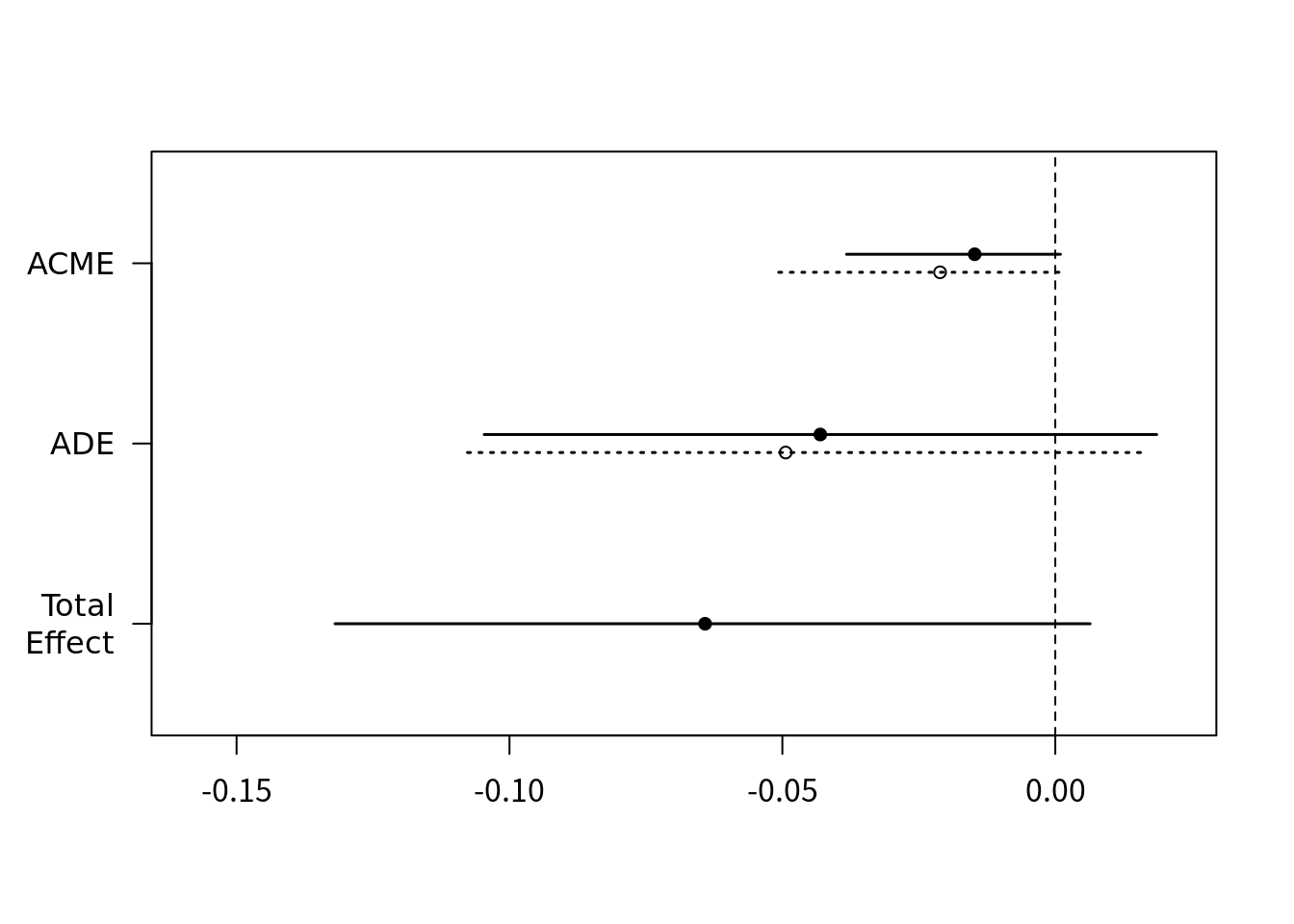

　結果を見るとtreat群とcontrol群でACMEの値に大きな違いは無さそう。したがって介入群と対照群ともに負のACMEを持つと考えられる。

おまけ：セミパラメトリックな解析方法（一般化加法モデル）

　アウトカムモデルに対して分布を仮定しないセミパラメトリックな方法もある。アウトカムを従属変数としたモデルにおいて、線形回帰の代わりに一般化加法モデルを使用する。
　mgcvパッケージのgam関数で一般化加法モデルによるモデル化が可能。s()の部分はスプラインでのモデル化を表現しており、bs=“cr”で3次基底関数でのモデル化（平滑化スプライン）を行っている。

library(mgcv)
##  要求されたパッケージ nlme をロード中です
## This is mgcv 1.8-34. For overview type 'help("mgcv-package")'.
model.y1 <- gam(depress2 ~ treat + s(job_seek,bs="cr") + econ_hard +
                 sex + age, data=jobs)
out1 <- mediate(model.m, model.y1, sims=100, boot=TRUE, treat="treat",
                mediator="job_seek")
## Running nonparametric bootstrap
plot(out1)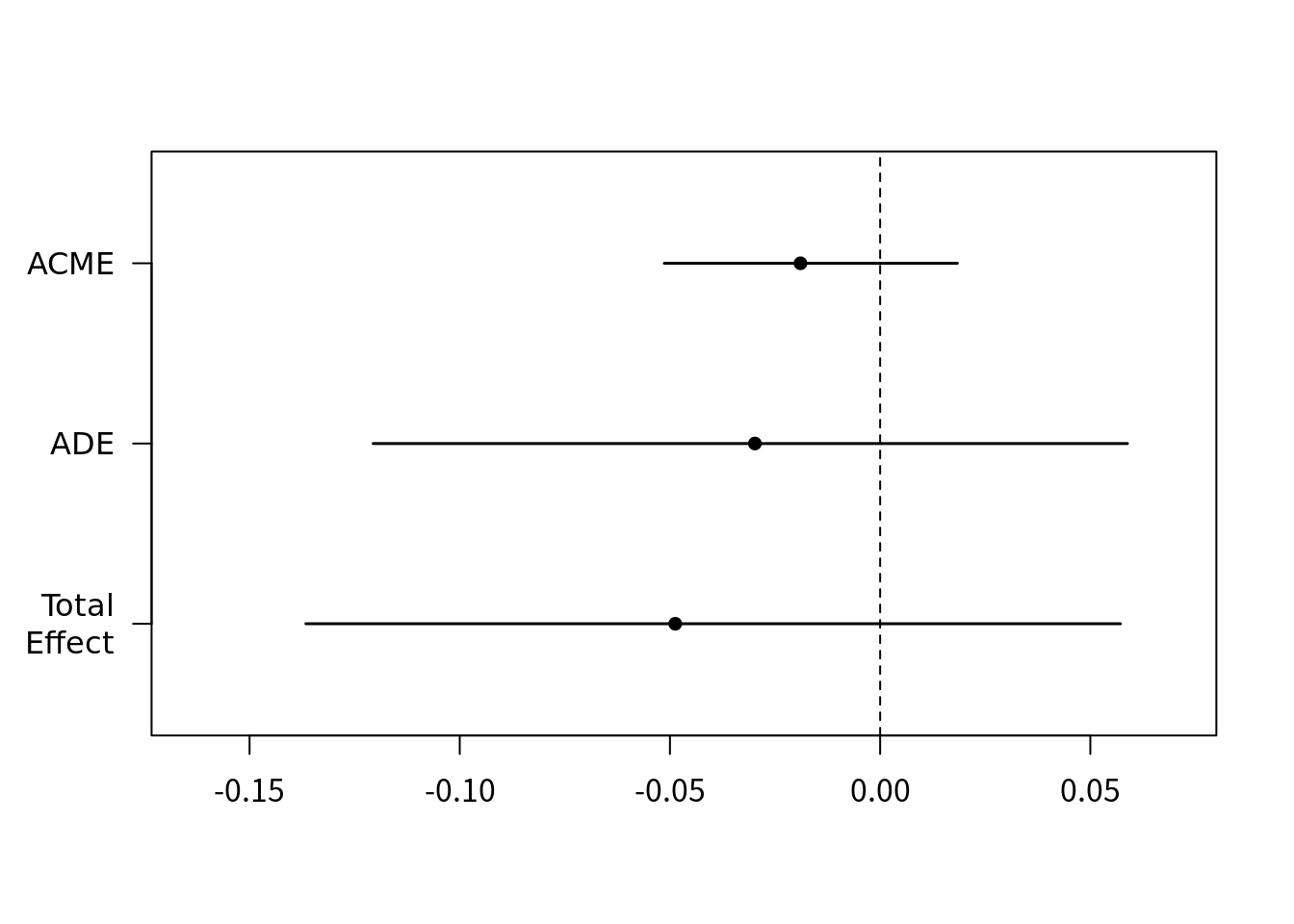

summary(out1)
## 
## Causal Mediation Analysis 
## 
## Nonparametric Bootstrap Confidence Intervals with the Percentile Method
## 
##                Estimate 95% CI Lower 95% CI Upper p-value
## ACME            -0.0189      -0.0513         0.02    0.24
## ADE             -0.0298      -0.1206         0.06    0.28
## Total Effect    -0.0487      -0.1366         0.06    0.22
## Prop. Mediated   0.3887      -2.2491         1.36    0.34
## 
## Sample Size Used: 899 
## 
## 
## Simulations: 100

終わりに

　以上Baron-Kenny法による因果媒介分析を扱い、実際のデータをもとにRコードで解析してみた。今回は媒介変数とアウトカムが連続変数の場合を扱った。この手法は厳しい仮定を置いてしまうものの、感度分析を行うことで解析結果が妥当であるか検討することができる。

参考文献

1. Advances in social science Research using R（第8章 Causal Mediation Analysis Using R）
2. Imai, K. et al. Identification, Inference and Sensitivity Aanalysis for Causal Mediation Effects. Statistical Science. 2010; 25(1):51-71.
3. Imai, K. et al. A General Approach to Causal Mediation Analysis. Phycological Methods. 2010;15(4):309-334.