今回は2値アウトカムに対する因果媒介分析を扱う。医学分野では解釈を容易にするため、カテゴリ化されたアウトカムを使用することが多い。カテゴリー変数をアウトカムとする場合、解析に使用するモデルもロジスティックやプロビットなどにする必要がある。前回と同様に解析と感度分析を行い、結果の解釈を行ってみる。

　前回と同様jobsデータを使用。介入をtreat（職業技能ワークショップへの参加）、連続媒介変数をjob_seek（就職活動自己効力感）、2値媒介変数をjob_cich（job_seekの値が4以上なら1、4未満なら0、として2値に変換）、アウトカムをwork1（ワークショップ参加後の就職）、交絡変数をecon_hard（経済的困難）・sex・ageとする。

　まずはデータの読み込みから。

library(mediation)
data("jobs")

連続媒介変数 + 2値アウトカム

　連続媒介変数（就職活動自己効力感）を応答変数とした重回帰分析を行う。これはBaron-Kenny法と同様。

m.con <- lm(job_seek ~ treat + econ_hard + sex + age, data=jobs)

　2値アウトカムwork1（ワークショップ後の就職）を応答変数、連続媒介変数job_seekと曝露変数treatを説明変数として、プロビット回帰を行う。glm関数を使用し、family引数でアウトカムに対して仮定する分布とリンク関数を指定できる（2値変数は2項分布に従うためbinomial、リンク関数はプロビット回帰）。

o.bin <- glm(work1 ~ treat + job_seek + econ_hard + sex + age, 
                 family=binomial(link="probit"),data=jobs)
conbin <- mediate(m.con, o.bin, sims=100, boot=TRUE,
                  treat="treat", mediator="job_seek")
## Running nonparametric bootstrap
summary(conbin)
## 
## Causal Mediation Analysis 
## 
## Nonparametric Bootstrap Confidence Intervals with the Percentile Method
## 
##                          Estimate 95% CI Lower 95% CI Upper p-value
## ACME (control)            0.00266     -0.00168         0.01    0.22
## ACME (treated)            0.00286     -0.00182         0.01    0.22
## ADE (control)             0.05413     -0.02045         0.11    0.14
## ADE (treated)             0.05433     -0.02055         0.11    0.14
## Total Effect              0.05699     -0.01709         0.11    0.14
## Prop. Mediated (control)  0.04665     -0.27222         0.18    0.36
## Prop. Mediated (treated)  0.05016     -0.26421         0.19    0.36
## ACME (average)            0.00276     -0.00175         0.01    0.22
## ADE (average)             0.05423     -0.02050         0.11    0.14
## Prop. Mediated (average)  0.04841     -0.26821         0.19    0.36
## 
## Sample Size Used: 899 
## 
## 
## Simulations: 100
plot(conbin)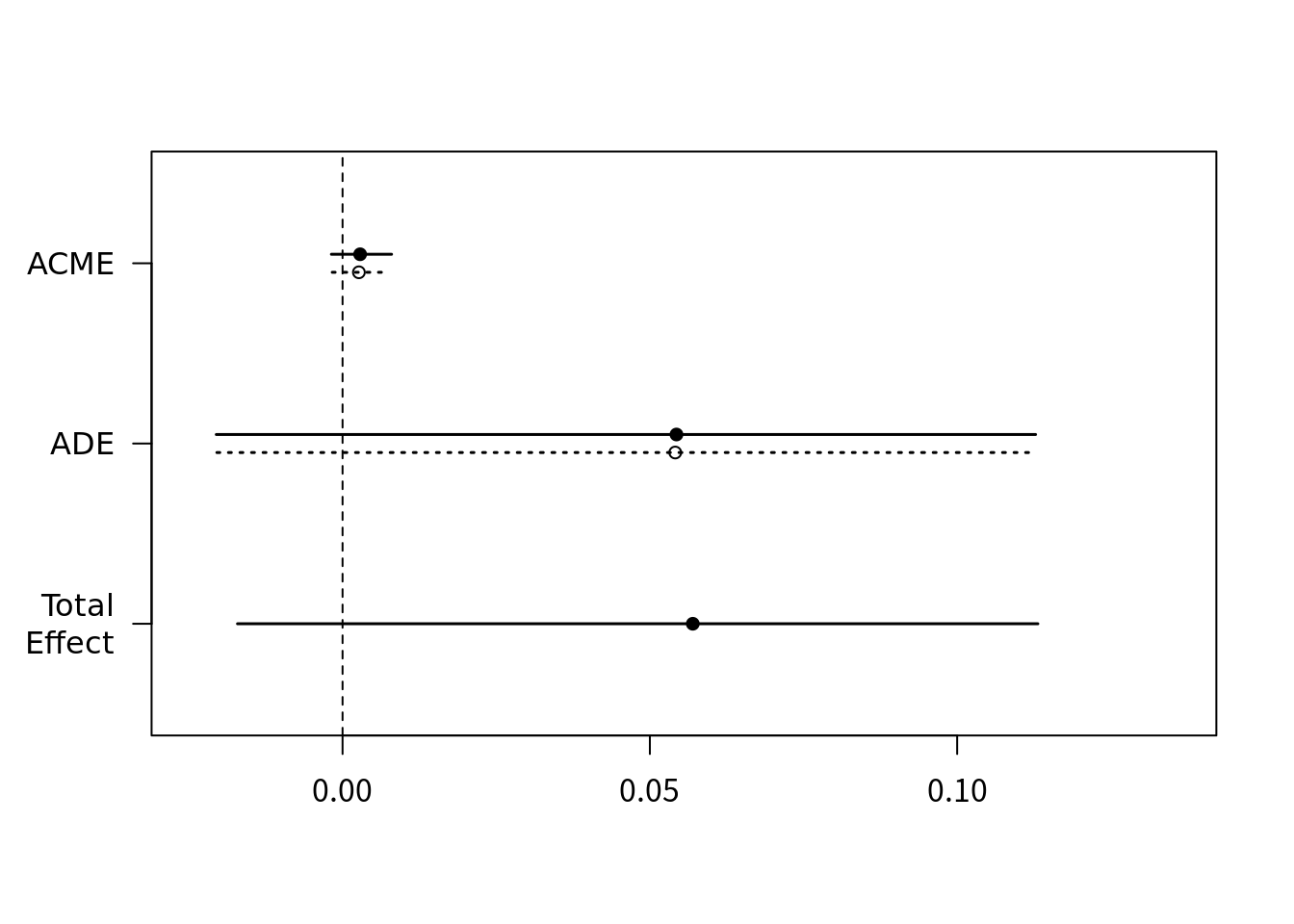

2値媒介変数 + 2値アウトカム

　媒介変数とアウトカムがともに2値変数の場合、両モデルにプロビット回帰を使用。

m.bin <- glm(job_dich ~ treat + econ_hard + sex + age, 
                 family=binomial(link="probit"),data=jobs)
o.bin <- glm(work1 ~ treat + job_dich + econ_hard + sex + age, 
                 family=binomial(link="probit"),data=jobs)
binbin <- mediate(m.bin, o.bin, sims=100, boot=TRUE, 
                  treat="treat", mediator="job_dich")
## Running nonparametric bootstrap
summary(binbin)
## 
## Causal Mediation Analysis 
## 
## Nonparametric Bootstrap Confidence Intervals with the Percentile Method
## 
##                           Estimate 95% CI Lower 95% CI Upper p-value
## ACME (control)            0.003661    -0.000930         0.01    0.12
## ACME (treated)            0.003895    -0.000929         0.01    0.12
## ADE (control)             0.052127    -0.020093         0.11    0.16
## ADE (treated)             0.052362    -0.020139         0.11    0.16
## Total Effect              0.056023    -0.018327         0.11    0.14
## Prop. Mediated (control)  0.065341    -0.787246         0.44    0.22
## Prop. Mediated (treated)  0.069532    -0.779056         0.44    0.22
## ACME (average)            0.003778    -0.000929         0.01    0.12
## ADE (average)             0.052245    -0.020116         0.11    0.16
## Prop. Mediated (average)  0.067437    -0.783151         0.44    0.22
## 
## Sample Size Used: 899 
## 
## 
## Simulations: 100
plot(binbin)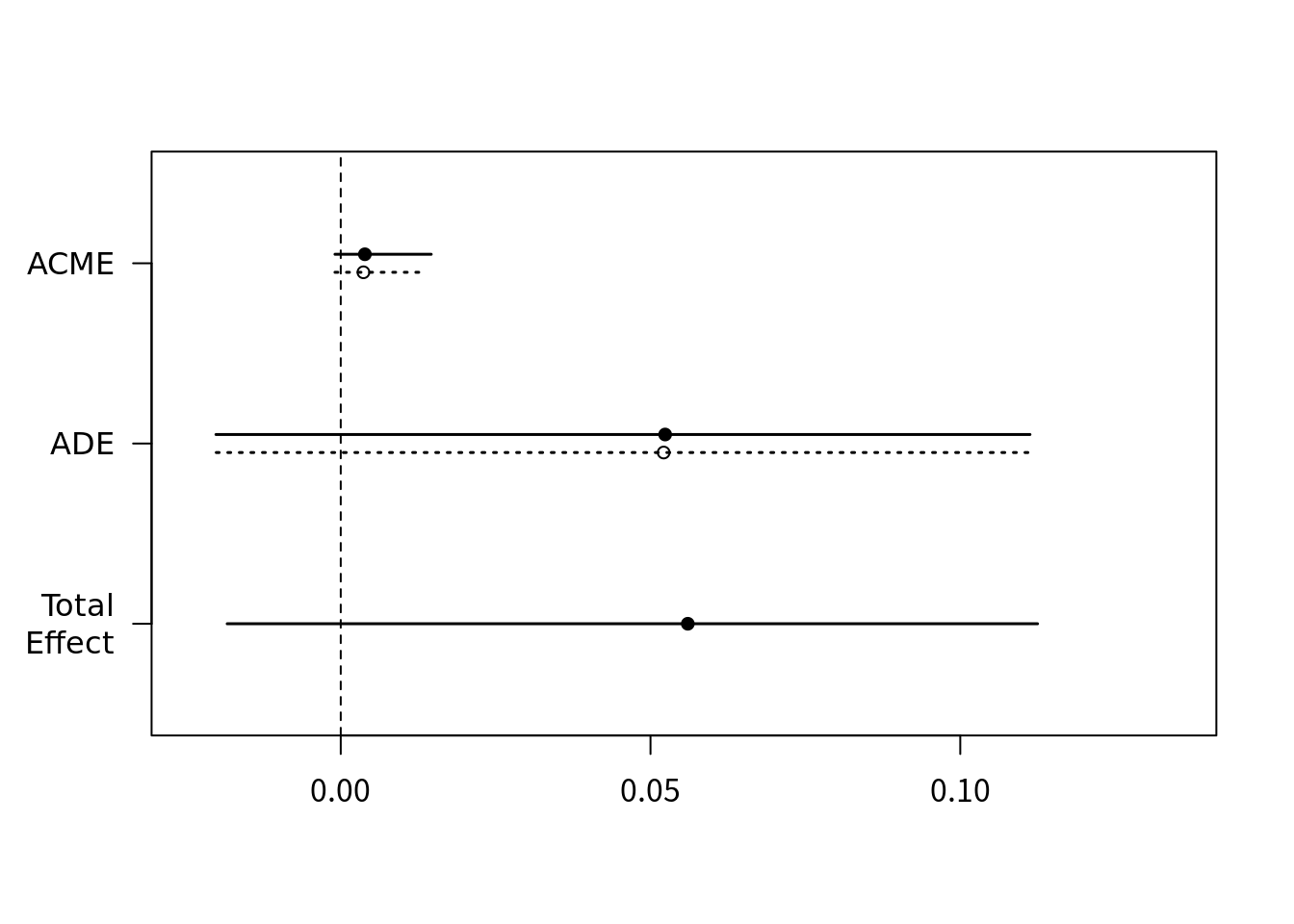

一応ロジスティックモデルも実行してみた。

m.binl <- glm(job_dich ~ treat + econ_hard + sex + age, 
                 family=binomial(link="logit"),data=jobs)
o.binl <- glm(work1 ~ treat + job_dich + econ_hard + sex + age, 
                 family=binomial(link="logit"),data=jobs)
binbinl <- mediate(m.binl, o.binl, sims=100, boot=TRUE, 
                  treat="treat", mediator="job_dich")
## Running nonparametric bootstrap
summary(binbinl)
## 
## Causal Mediation Analysis 
## 
## Nonparametric Bootstrap Confidence Intervals with the Percentile Method
## 
##                           Estimate 95% CI Lower 95% CI Upper p-value
## ACME (control)            0.001931    -0.000400         0.01    0.12
## ACME (treated)            0.002077    -0.000470         0.02    0.12
## ADE (control)             0.051301    -0.010999         0.12    0.14
## ADE (treated)             0.051446    -0.011113         0.12    0.14
## Total Effect              0.053378    -0.004578         0.12    0.10
## Prop. Mediated (control)  0.036182    -0.596896         0.57    0.18
## Prop. Mediated (treated)  0.038907    -0.583680         0.58    0.18
## ACME (average)            0.002004    -0.000435         0.02    0.12
## ADE (average)             0.051374    -0.011056         0.12    0.14
## Prop. Mediated (average)  0.037544    -0.590288         0.58    0.18
## 
## Sample Size Used: 899 
## 
## 
## Simulations: 100
plot(binbinl)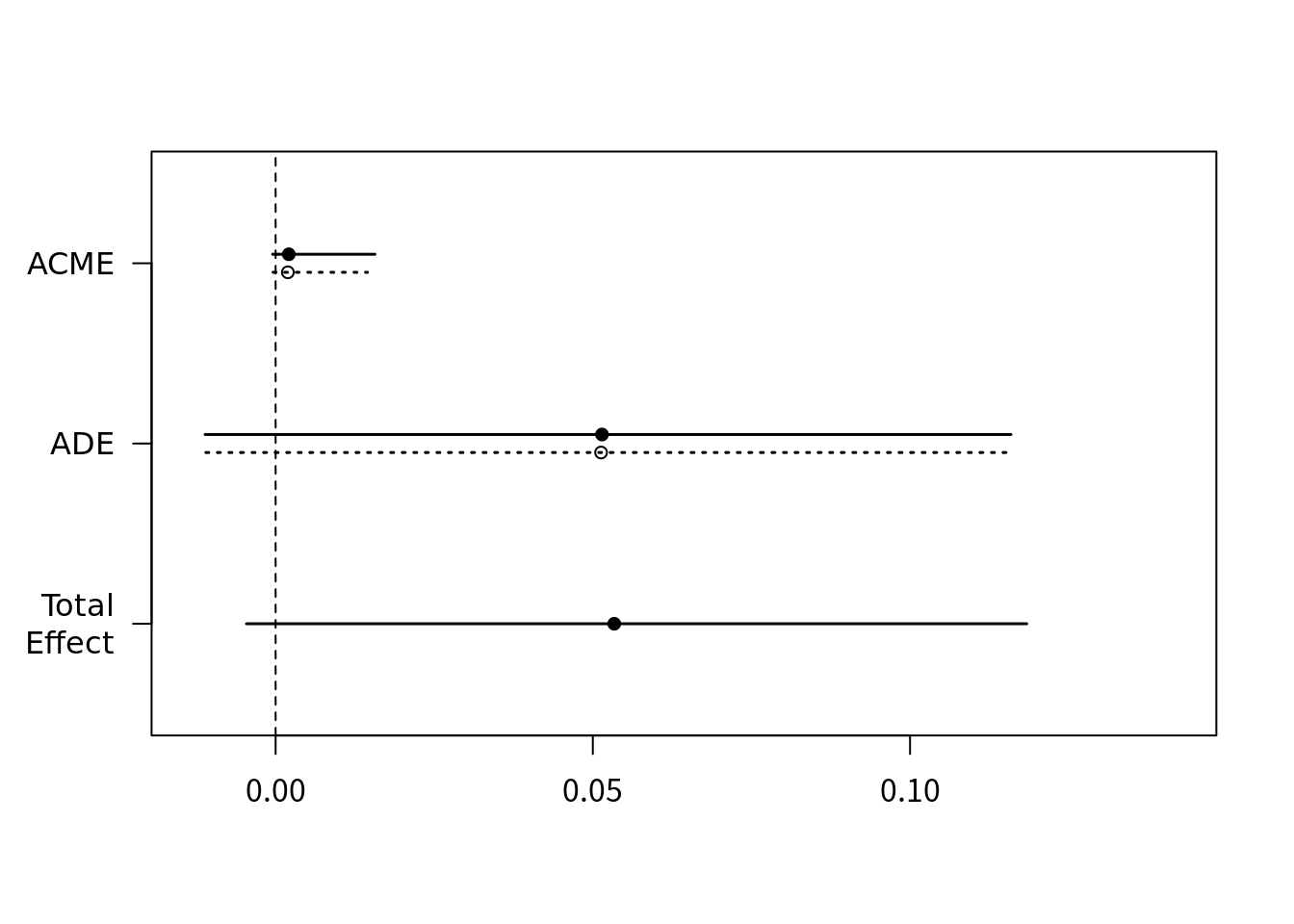

　プロビット、ロジスティックモデルでの結果を見ると、平均因果媒介効果(ACME)の点推定値と信頼区間が正の大部分を被覆している。したがってワークショップは参加者の自己効力感を増し、就職につながった可能性があることがわかった（ただ点推定値が小さいのは気になるところ）。ただ上記の解析は、未測定交絡の問題や交互作用について無視したものである点は注意すべきである。

未測定交絡の感度分析

　連続媒介変数と2値アウトカムの場合のみ感度分析を行う（2値アウトカムを含む他の組は解析不可）。

連続媒介変数＋2値アウトカム

　感度分析はmedsens関数で行う。媒介分析の結果が入ったオブジェクトconbin、有意水準、信頼区間を計算するためのブートストラップ法の試行回数を指定。まず相関係数による感度分析を実行する。

sens.conbin <- medsens(conbin, rho.by=0.05, sims=100)
## Warning in rho^2 * (1 - r.sq.m) * (1 - r.sq.y): Recycling array of length 1 in vector-array arithmetic is deprecated.
##   Use c() or as.vector() instead.
## Warning in err.cr.d^2 * (1 - r.sq.m) * (1 - r.sq.y): Recycling array of length 1 in vector-array arithmetic is deprecated.
##   Use c() or as.vector() instead.
plot(sens.conbin, sens.par="rho")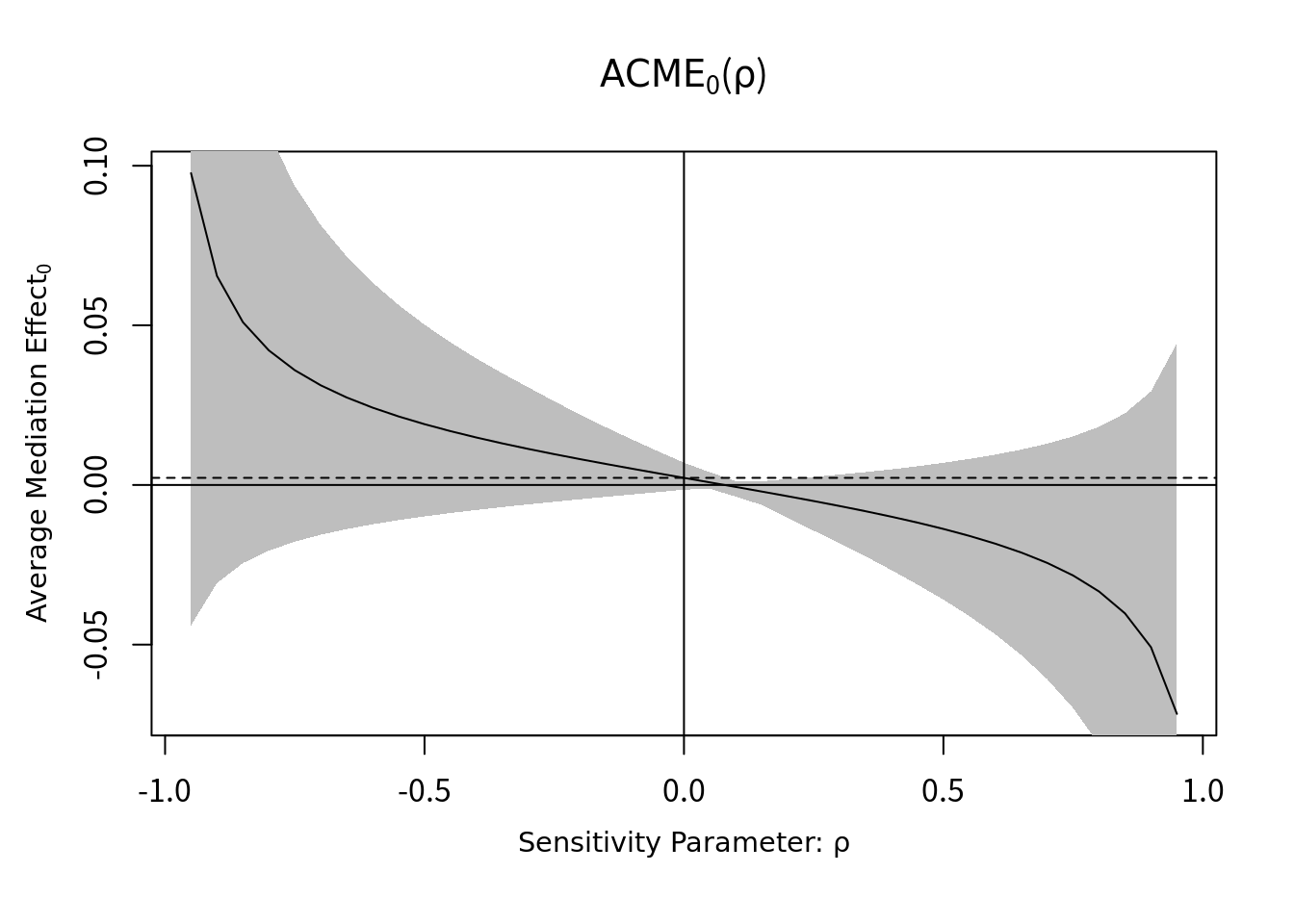

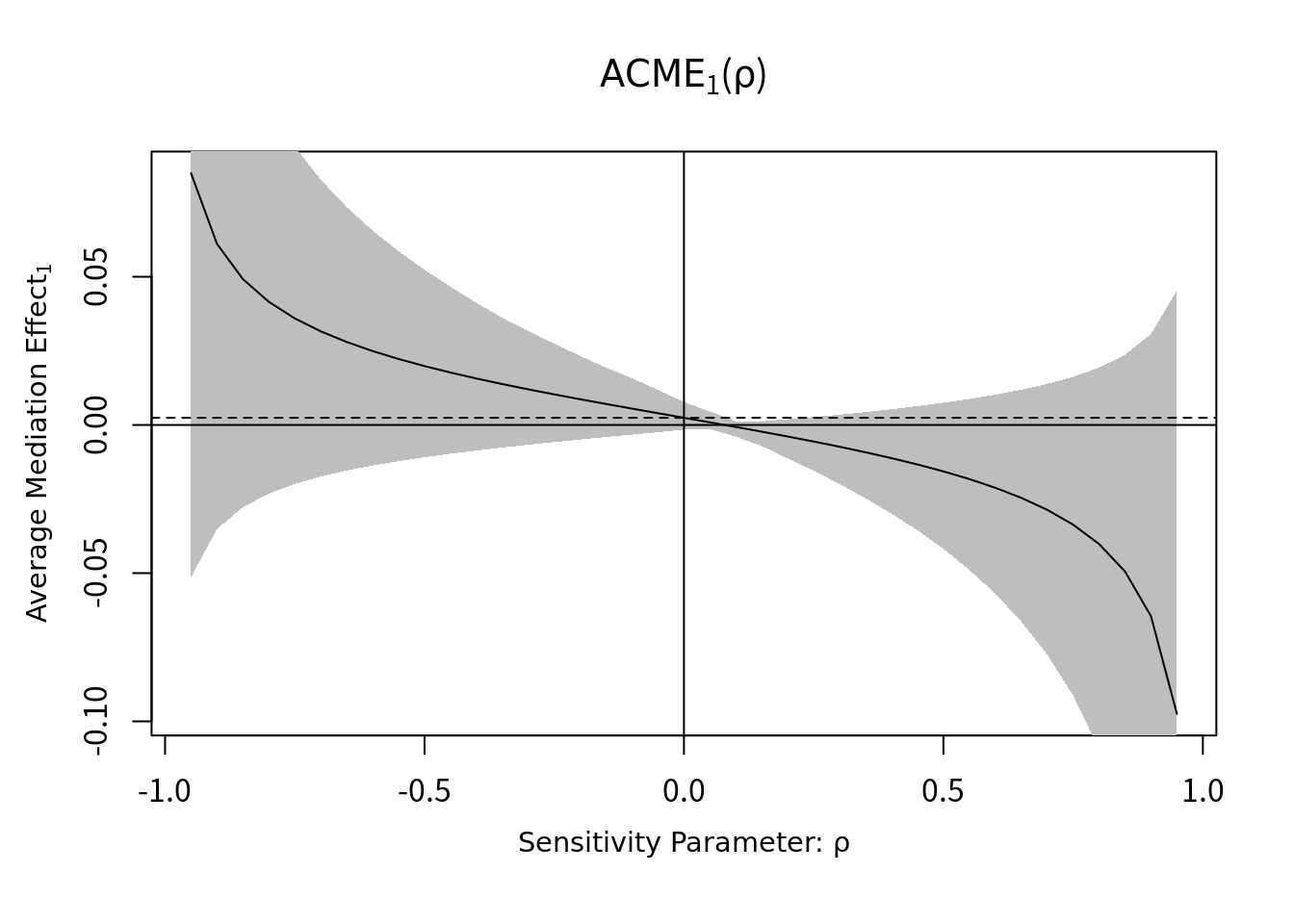　 　感度分析の結果の見方は、①点線は、Sequencial ignorability下（未測定交絡なしというあまりにも厳しい仮定）でのACME（平均因果媒介効果）の点推定値、②曲線は、未測定交絡による相関に対応したACME、③グレーは、ACMEの95%信頼区間、を示す。
　相関係数は解釈が難しいので、決定係数による感度分析も実行する。

plot(sens.conbin, sens.par="R2", r.type=2, sign.prod = 1)
## Warning in (1 - x$r.square.y) * seq(0, 1 - x$rho.by, 0.01): Recycling array of length 1 in array-vector arithmetic is deprecated.
##   Use c() or as.vector() instead.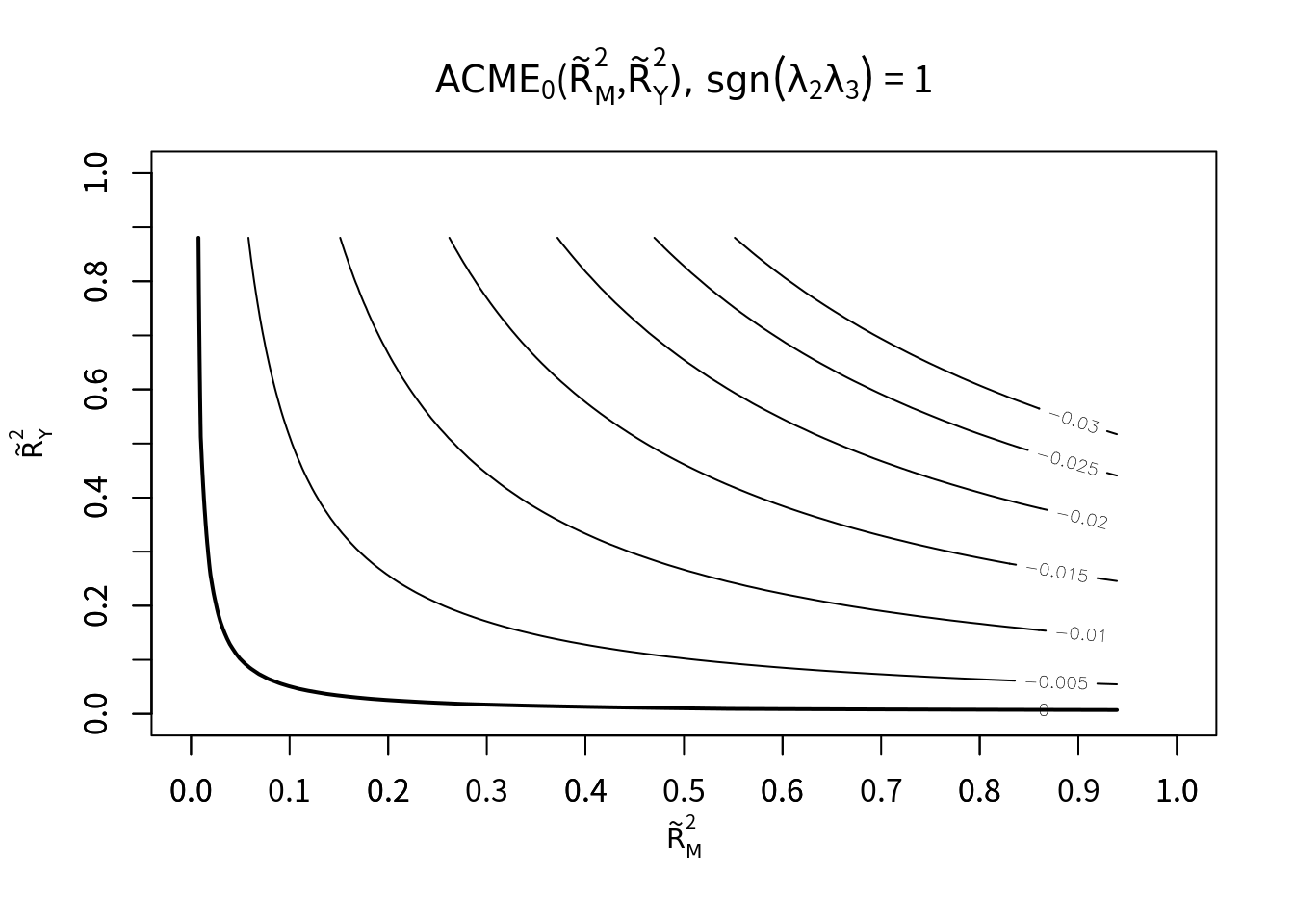

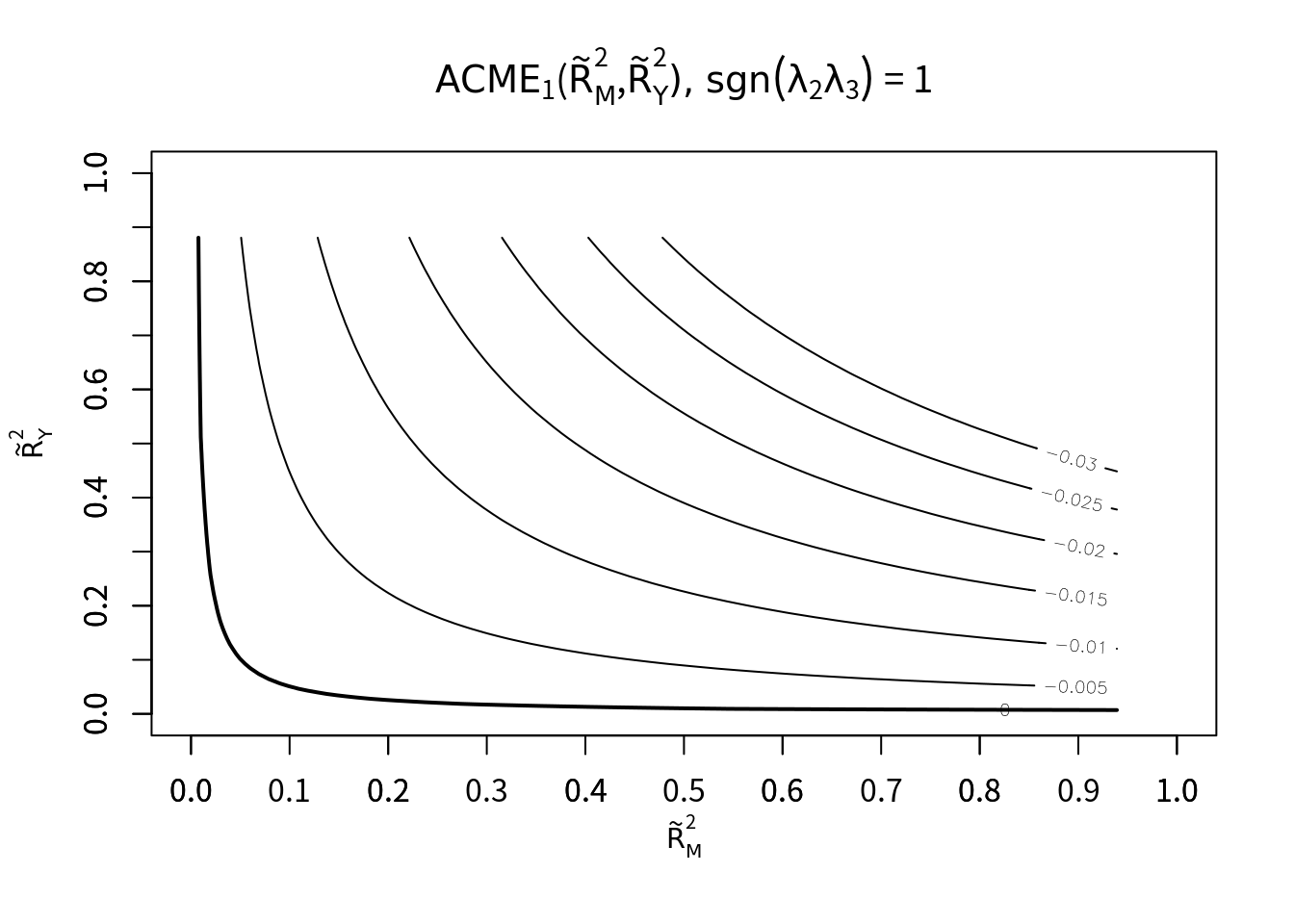
plot(sens.conbin, sens.par="R2", r.type=2, sign.prod = -1)
## Warning in (1 - x$r.square.y) * seq(0, 1 - x$rho.by, 0.01): Recycling array of length 1 in array-vector arithmetic is deprecated.
##   Use c() or as.vector() instead.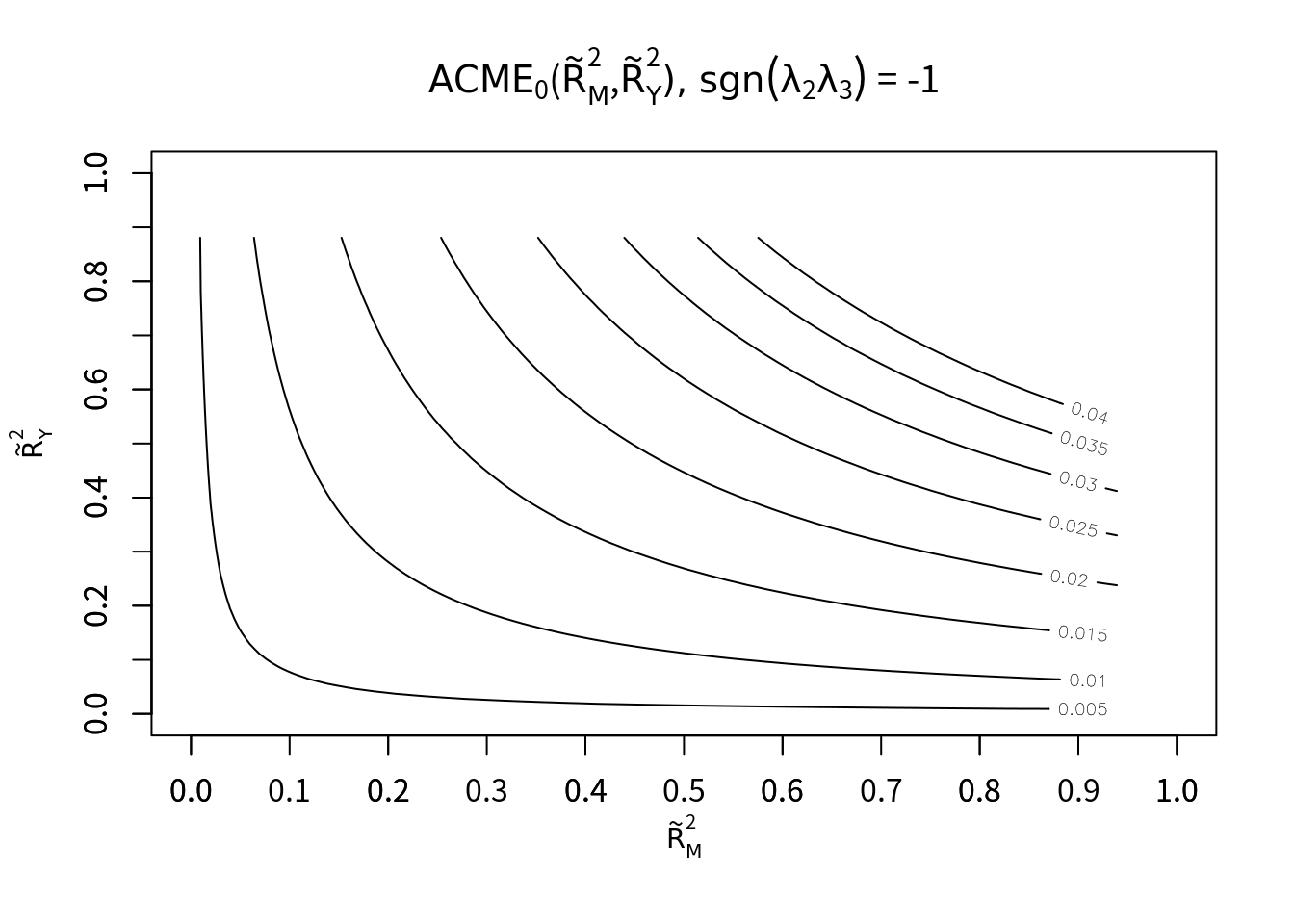

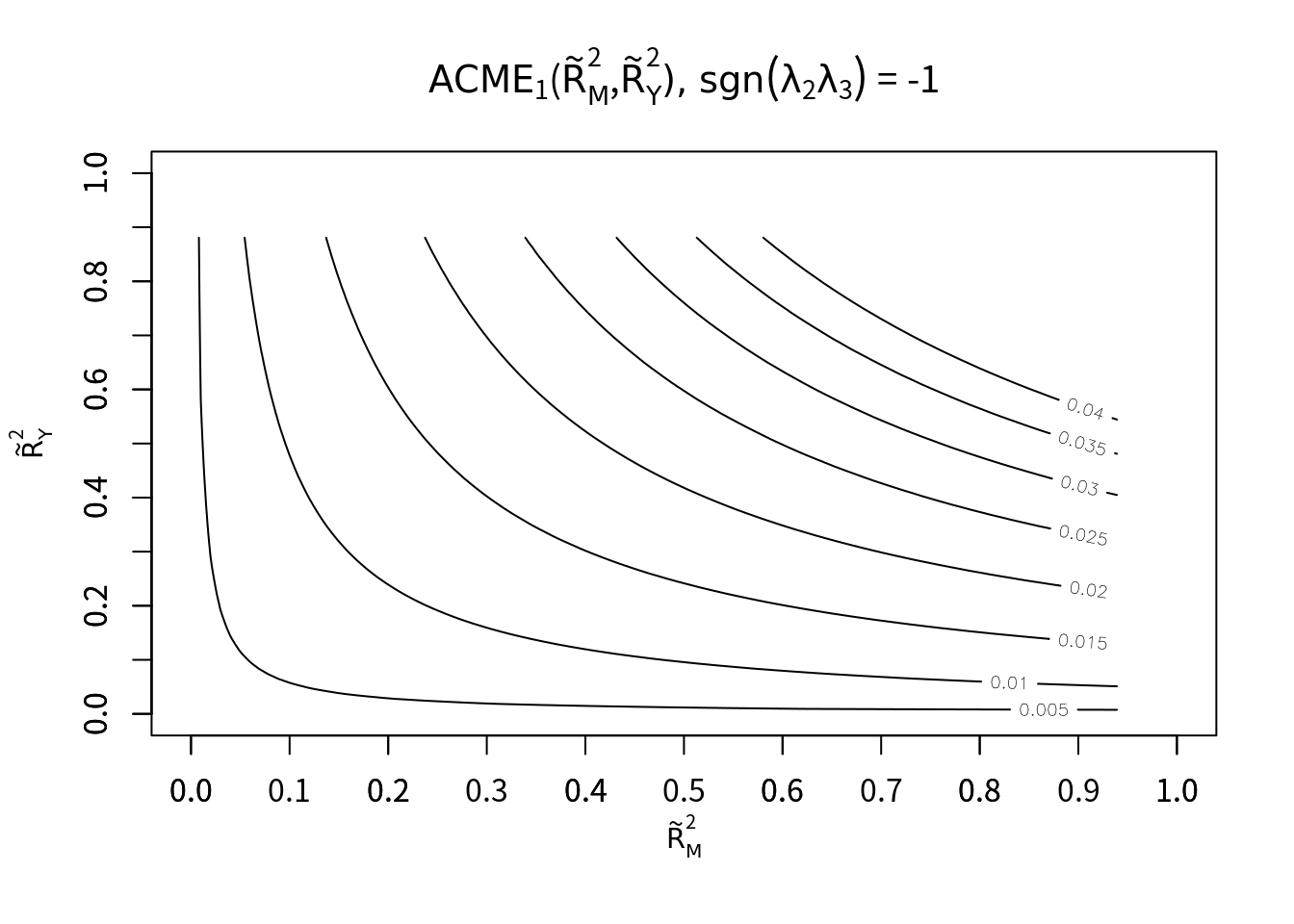　決定係数の感度分析の結果をみると、未測定交絡が媒介変数・アウトカムに対してどの符号で相関をもつのかによって、結果が変わることが分かる。ただいずれも場合でも、ACMEの点推定値は正もしくは負の一貫した符号を持っている。つまり未測定交絡があったとしても、媒介効果は存在すると考えられる（符号がどっちかは不明だが）。

　ただし点推定値があまり大きい値ではないため、実際にどの程度の影響なのかは考慮が必要だろう。例えば、未測定交絡含めACMEは0.02だったとしよう。この0.02という値は、職業訓練ワークショプが参加者の自己効力感を高めて就職につなげたと考えて良い値なのだろうか。正直なところ、ちょっと怪しかったりする。総効果に対する媒介効果の割合が小さいことから、もしかしたら他の要因が関わっている可能性もあるだろう。なんらかの有益な知識、就活のテクニックを得ることができたとか。

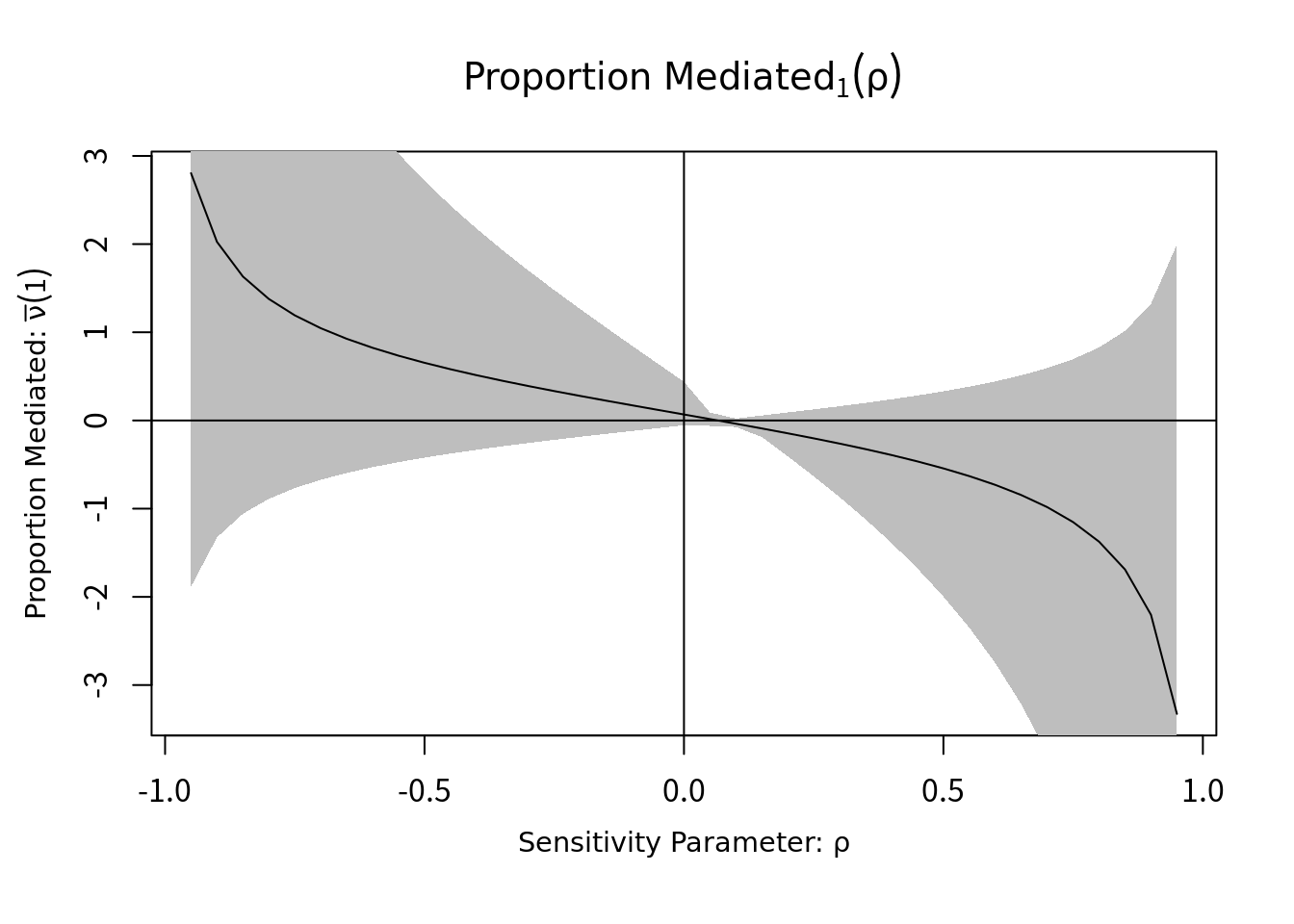
　ちなみに2値アウトカムの場合、媒介効果の割合も出力できる。

plot(sens.conbin, sens.par="rho", pr.plot = TRUE)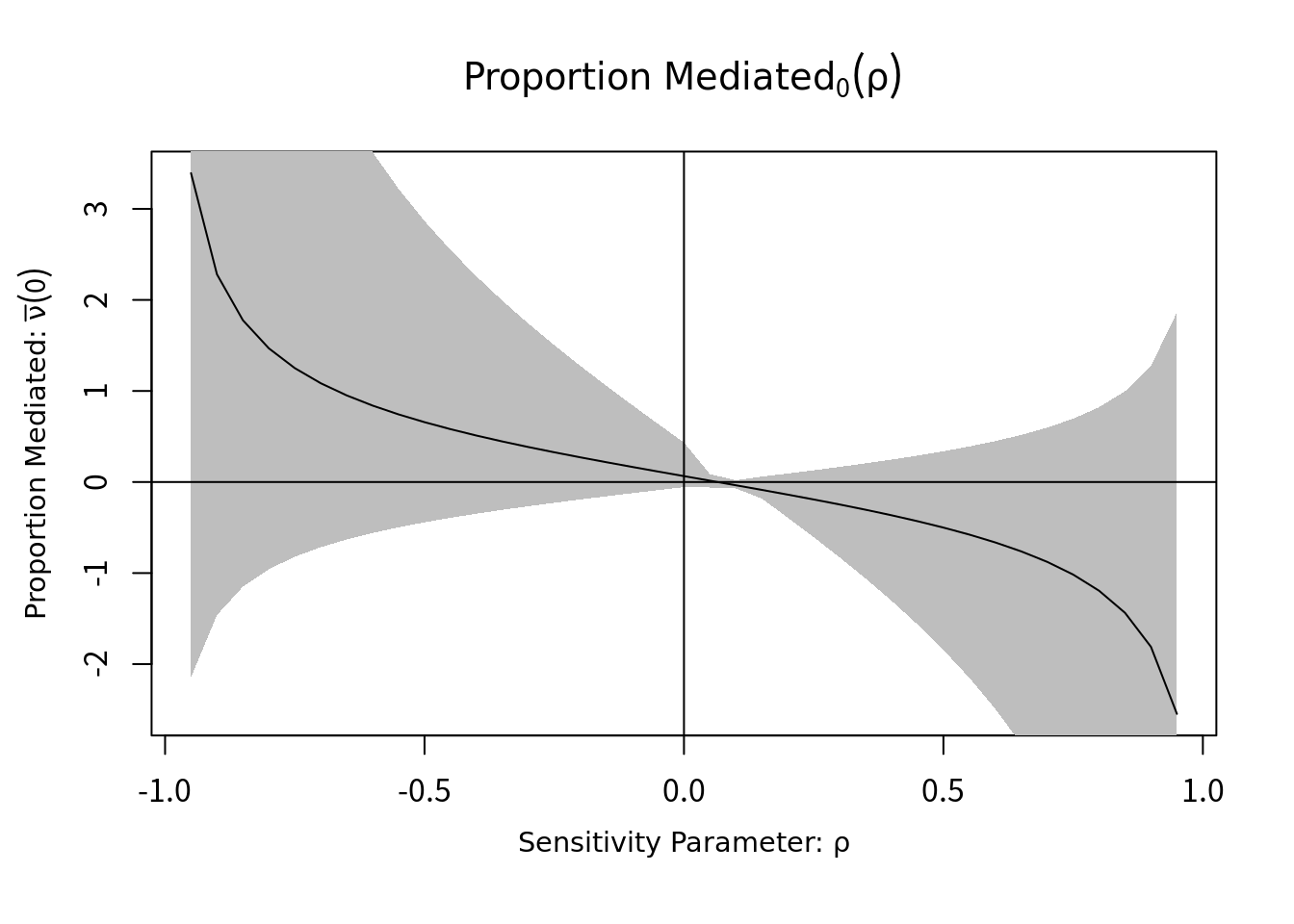

plot関数 内容
sens.par=“R2” 決定係数による感度分析（デフォルトは相関係数）
r.type=1　　 未測定交絡によって説明される原因不明の分散比率での感度分析
　　　=2 未測定交絡によって説明される元の分散比率での感度分析
sign.prod=1 未測定交絡の係数符号が媒介変数・アウトカムで同じ場合
　　　　=-1 係数の符号が異なるもとでの感度分析 　
pr.plot=TRUE 総効果のうち、媒介される割合（2値アウトカムのみ可）

解析可能な媒介変数・アウトカムの組み合わせ

　Rのmediationパッケージで解析可能な変数型の組み合わせを以下に示す。媒介分析については、順序アウトカムの解析は不可能。また感度分析が行える組み合わせも少ない。

媒介分析 連続アウトカム 順序アウトカム 2値アウトカム
媒介変数：連続 ○ 　 × ○
媒介変数：順序 ○ × ×
媒介変数：2値 ○ × ○
感度分析 連続アウトカム 順序アウトカム 2値アウトカム
媒介変数：連続 ○ 　 × ○
媒介変数：順序 × × ×
媒介変数：2値 ○ × ×

参考文献

1. Advances in social science Research using R（第8章 Causal Mediation Analysis Using R）
2. Imai, K. et al. Identification, Inference and Sensitivity Aanalysis for Causal Mediation Effects. Statistical Science. 2010; 25(1):51-71.
3. Imai, K. et al. A General Approach to Causal Mediation Analysis. Phycological Methods. 2010;15(4):309-334.