「相関≠因果」は統計学本でよく目にします。これは正しいのですが、不正確な表現です。正確には、「特定の条件下で、相関=因果」が正しいです。ではその特定の条件下とは何か。それを扱うのが因果推論という統計学の分野です。
「相関≠因果」を生じさせる原因の一つが交絡と呼ばれる現象です。以下でデータを扱いながら考えましょう。
「相関=因果」の状態
まず「相関=因果」となっている状態をデータで表現してみます。Aが曝露(原因)、Yがアウトカム(結果)とします。
set.seed(100)
d1 <- data.frame(A=rbinom(1000,1,0.5))
for(i in 1:1000){
ifelse(d1[i,1]==1, d1[i,2] <- rbinom(1,1,0.7),d1[i,2] <- rbinom(1,1,0.3))
}
names(d1)[which(names(d1)=="V2")] <- "Y"library(dagitty)
g <- dagitty('dag{
A -> Y
}')
coordinates(g) <- list(x=c(A=0,Y=1),y=c(A=0,Y=0))
plot(g)
作成したデータでは、AはYに対して因果関係にあると言えます。以下の棒グラフでは、A=1とA=0でのYの分布(Y=1とY=0)を示していますが、AはYに対して因果関係があるので、A=1の方がY=1の割合は高くなっています。ちなみにAはYに対してリスク比2.3[2.0 - 2.6]、リスク差38.0%[32.2 - 43.7]のリスクを持っています(いずれも有意)。
library(epiR)
library(epitools)
table(d1)# Y
# A 0 1
# 0 333 151
# 1 159 357table1 <- xtabs(~Y+A, data=d1)
barplot(table1, legend=rownames(table1))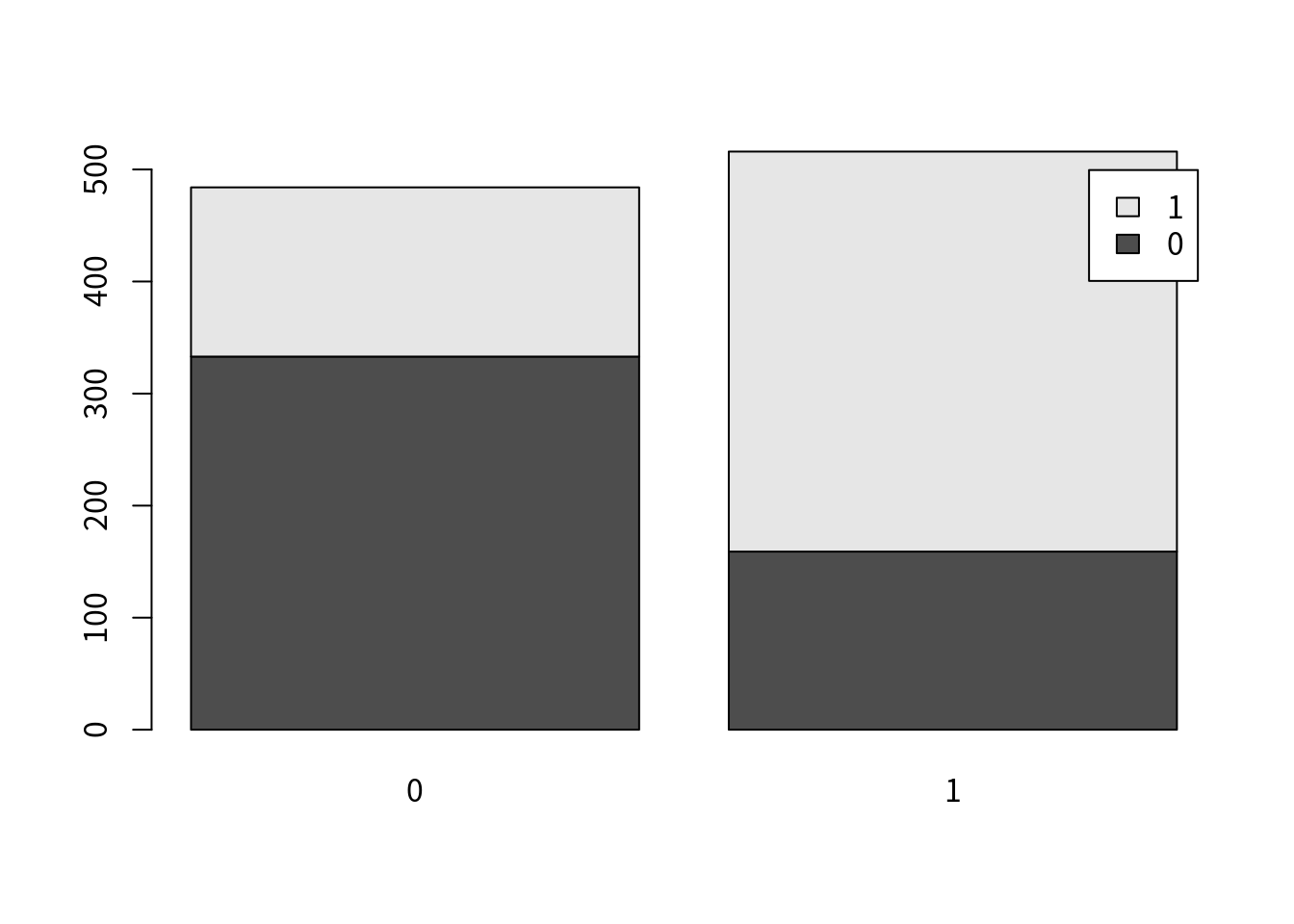
epi.2by2(table1)# Outcome + Outcome - Total Inc risk * Odds
# Exposed + 333 159 492 67.7 2.094
# Exposed - 151 357 508 29.7 0.423
# Total 484 516 1000 48.4 0.938
#
# Point estimates and 95% CIs:
# -------------------------------------------------------------------
# Inc risk ratio 2.28 (1.97, 2.64)
# Odds ratio 4.95 (3.79, 6.47)
# Attrib risk * 37.96 (32.22, 43.69)
# Attrib risk in population * 18.68 (13.64, 23.71)
# Attrib fraction in exposed (%) 56.08 (49.13, 62.09)
# Attrib fraction in population (%) 38.59 (31.85, 44.65)
# -------------------------------------------------------------------
# Test that OR = 1: chi2(1) = 144.196 Pr>chi2 = <0.001
# Wald confidence limits
# CI: confidence interval
# * Outcomes per 100 population units「相関≠因果」の状態
では先程とは別のデータを新たに作ります。
d2 <- data.frame(L=rnorm(1000,45,15))
for(i in 1:1000){
ifelse(d2[i,1]>60, d2[i,2] <- rbinom(1,1,0.8), d2[i,2] <- rbinom(1,1,0.3))
ifelse(d2[i,1]>60, d2[i,3] <- rbinom(1,1,0.8), d2[i,3] <- rbinom(1,1,0.3))
}
names(d2)[which(names(d2)=="V2")] <- "A"
names(d2)[which(names(d2)=="V3")] <- "Y"実は今回作成したデータでは、AはYに対して因果関係を持っていません。なぜならAとYは、第3の変数Lによってデータが生成されたからです。
library(dagitty)
g <- dagitty('dag{
L -> Y
L -> A
}')
coordinates(g) <- list(x=c(A=0,L=0.5,Y=1),y=c(A=0,L=1,Y=0))
plot(g)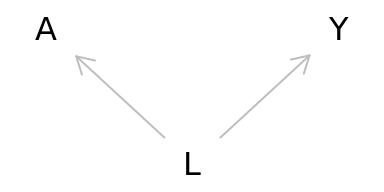
また先程と同様にリスク比とリスク差を計算してみます。
library(epiR)
library(epitools)
table2 <- xtabs(~Y+A, data=d2)
barplot(table2, legend=rownames(table2))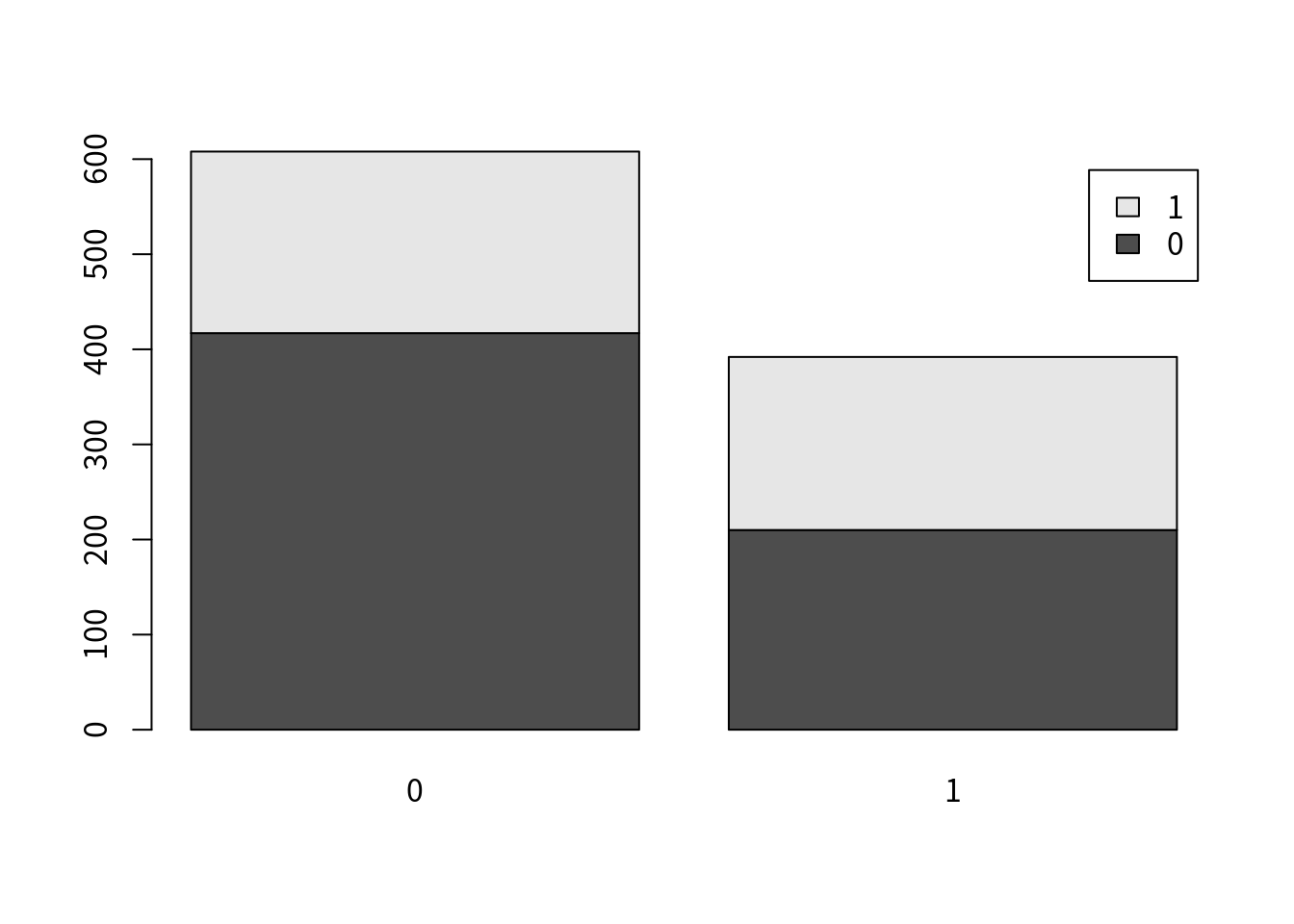
epi.2by2(table2)# Outcome + Outcome - Total Inc risk * Odds
# Exposed + 417 210 627 66.5 1.99
# Exposed - 191 182 373 51.2 1.05
# Total 608 392 1000 60.8 1.55
#
# Point estimates and 95% CIs:
# -------------------------------------------------------------------
# Inc risk ratio 1.30 (1.16, 1.46)
# Odds ratio 1.89 (1.46, 2.46)
# Attrib risk * 15.30 (9.03, 21.58)
# Attrib risk in population * 9.59 (3.69, 15.50)
# Attrib fraction in exposed (%) 23.01 (13.75, 31.27)
# Attrib fraction in population (%) 15.78 (8.92, 22.12)
# -------------------------------------------------------------------
# Test that OR = 1: chi2(1) = 22.973 Pr>chi2 = <0.001
# Wald confidence limits
# CI: confidence interval
# * Outcomes per 100 population units上記の結果を見ると、AはYに対して因果関係に無いにも関わらず、ぞれぞれリスク比1.3[1.2 - 1.5]、リスク差15.3%[9.0 - 21.6]となっています。あたかもAがYに対して因果関係を持っているように見えます。これが交絡と呼ばれる現象です。
交絡への対処
もし仮に交絡がLによって生じていると判明している場合、実はいくつかの方法で対処できます。今回は3つ紹介します。
データの作成段階でLは60を境に曝露とアウトカムに影響することが分かっているので、Lを60より上、以下で2つの層に分けておきます。
for(i in 1:1000){
ifelse(d2[i,1]>60, d2[i,4] <- 1, d2[i,4] <- 0)
}
names(d2)[4] <- "L60"1. MHの方法による調整リスク比・リスク差の計算
まずMH(マンテルヘンツェル)の方法で調整リスク比、調整リスク差を計算してみます。
table3 <- xtabs(~Y+A+L60,data=d2)
epi.2by2(table3)# Outcome + Outcome - Total Inc risk * Odds
# Exposed + 417 210 627 66.5 1.99
# Exposed - 191 182 373 51.2 1.05
# Total 608 392 1000 60.8 1.55
#
#
# Point estimates and 95% CIs:
# -------------------------------------------------------------------
# Inc risk ratio (crude) 1.30 (1.16, 1.46)
# Inc risk ratio (M-H) 0.99 (0.90, 1.09)
# Inc risk ratio (crude:M-H) 1.31
# Odds ratio (crude) 1.89 (1.46, 2.46)
# Odds ratio (M-H) 0.97 (0.71, 1.32)
# Odds ratio (crude:M-H) 1.96
# Attrib risk (crude) * 15.30 (9.03, 21.58)
# Attrib risk (M-H) * -0.70 (-9.85, 8.45)
# Attrib risk (crude:M-H) -21.80
# -------------------------------------------------------------------
# M-H test of homogeneity of RRs: chi2(1) = 0.242 Pr>chi2 = 0.62
# M-H test of homogeneity of ORs: chi2(1) = 0.391 Pr>chi2 = 0.53
# Test that M-H adjusted OR = 1: chi2(1) = 0.048 Pr>chi2 = 0.83
# Wald confidence limits
# M-H: Mantel-Haenszel; CI: confidence interval
# * Outcomes per 100 population units上記の結果を見ると、MHリスク比は0.99、MHリスク差は-0.7%となっています。つまりLによって生じていた交絡を統制し、純粋なAとYの関係を見ることができたことになります。この結果から、AはYに対して因果関係に無いと確認することができました。
2. ロジスティックモデルによる調整オッズ比の計算
ロジスティック回帰を使用することで、交絡の影響を除いたオッズ比を計算できます。この方法の利点は、共変量に入れる変数が増えても調整オッズ比が計算できる点にあります。先程のMHの方法では、統制できる変数の数は非常に限られます。
L60を説明変数に加えて、
logistic <- glm(Y~A+L60, family="binomial", data=d2)
summary(logistic)#
# Call:
# glm(formula = Y ~ A + L60, family = "binomial", data = d2)
#
# Deviance Residuals:
# Min 1Q Median 3Q Max
# -1.8314 -0.8293 -0.8172 0.6534 1.5870
#
# Coefficients:
# Estimate Std. Error z value Pr(>|z|)
# (Intercept) -0.89073 0.09014 -9.882 <2e-16 ***
# A -0.03464 0.15848 -0.219 0.827
# L60 2.36086 0.22985 10.271 <2e-16 ***
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# (Dispersion parameter for binomial family taken to be 1)
#
# Null deviance: 1321.1 on 999 degrees of freedom
# Residual deviance: 1165.5 on 997 degrees of freedom
# AIC: 1171.5
#
# Number of Fisher Scoring iterations: 4exp(coef(logistic)) #調整オッズ比の点推定値# (Intercept) A L60
# 0.4103548 0.9659520 10.6000873exp(confint(logistic)) #信頼区間の上限・下限# Waiting for profiling to be done...# 2.5 % 97.5 %
# (Intercept) 0.3431507 0.488691
# A 0.7056189 1.314124
# L60 6.8401512 16.877911ここで得られた係数をオッズ比に変換する必要があります。なのでexp(-0.03)を計算して、調整オッズ0.97が得られます。信頼区間の下限と上限も同様にして計算できます。
3. 層別化による交絡の統制(層別化)
これが最もシンプルな方法です。単純にL60の2つの層でそれぞれリスク比・リスク差・オッズ比を計算するので、層別化と呼ばれます。各層でのリスク比・リスク差・オッズ比を計算できるので、層ごとの比較ができるのも大きな利点です(性別で層別化を行って比較をしている論文は非常に多いです)。
L1 <- subset(d2,L60==1)
L0 <- subset(d2,L60==0)
tableL1 <- xtabs(~Y+A, data=L1)
tableL0 <- xtabs(~Y+A, data=L0)
epi.2by2(tableL1)# Outcome + Outcome - Total Inc risk * Odds
# Exposed + 6 25 31 19.4 0.240
# Exposed - 21 110 131 16.0 0.191
# Total 27 135 162 16.7 0.200
#
# Point estimates and 95% CIs:
# -------------------------------------------------------------------
# Inc risk ratio 1.21 (0.53, 2.74)
# Odds ratio 1.26 (0.46, 3.44)
# Attrib risk * 3.32 (-11.94, 18.59)
# Attrib risk in population * 0.64 (-7.87, 9.15)
# Attrib fraction in exposed (%) 17.18 (-87.77, 63.47)
# Attrib fraction in population (%) 3.82 (-15.42, 19.84)
# -------------------------------------------------------------------
# Test that OR = 1: chi2(1) = 0.199 Pr>chi2 = 0.66
# Wald confidence limits
# CI: confidence interval
# * Outcomes per 100 population unitsepi.2by2(tableL0)# Outcome + Outcome - Total Inc risk * Odds
# Exposed + 411 185 596 69.0 2.22
# Exposed - 170 72 242 70.2 2.36
# Total 581 257 838 69.3 2.26
#
# Point estimates and 95% CIs:
# -------------------------------------------------------------------
# Inc risk ratio 0.98 (0.89, 1.08)
# Odds ratio 0.94 (0.68, 1.30)
# Attrib risk * -1.29 (-8.14, 5.57)
# Attrib risk in population * -0.92 (-7.47, 5.64)
# Attrib fraction in exposed (%) -1.87 (-12.37, 7.65)
# Attrib fraction in population (%) -1.32 (-8.60, 5.47)
# -------------------------------------------------------------------
# Test that OR = 1: chi2(1) = 0.134 Pr>chi2 = 0.71
# Wald confidence limits
# CI: confidence interval
# * Outcomes per 100 population units層別化はシンプルな方法ではありますが、サンプルサイズが小さくなりやすいことが問題となります。実際Lが60より上の層では、リスク比1.2[0.5 - 2.7]とリスク差3.32[-11.9 - 18.6]となっていて、信頼区間が広すぎます。今回の場合は明らかにサンプルサイズが足りていないので、妥当な方法とは言えません。
交絡の統制の難しさ
上記では交絡因子(交絡を引き起こす因子)Lが事前に分かっていたので、交絡の影響を除いたリスク比・リスク差・オッズ比が計算できました。しかし実際の調査やリアルワールドデータ、ビッグデータには、交絡因子は無数に存在しています。加えて交絡因子がすべて測定されているかもしくは既知であるかも私達には検証するすべがありません。ここが交絡のやっかいなところで、いくら交絡因子を列挙して統制しても、得られたAとYの関係が交絡によるものなのか、因果関係なのかが分からないのです。研究・解析を行う人間がすべきなのは、既存の学問的知見や一般常識の観点から、交絡因子を列挙して統制することです。
しかし「相関≠因果」をもたらすのは交絡だけではありません。間違った変数の統制や測定で生じるバイアスも問題となります。次回はこれら系統誤差を取り上げていきたいと思います。
